基于特征构建的区域电力负荷增长归因及量化分析方法

编者按

电力负荷分析是电力系统规划、运行和管理中不可或缺的一环，能够为电力系统高效、可靠和可持续运行提供关键信息。2023年4月25日，国家发改委向国家电网公司、南方电网公司、内蒙古电力公司下发《关于进一步加强用电监测分析工作的函》，要求加强重点行业用电监测分析，加强对夏季降温负荷、冬季采暖负荷等重要负荷监测分析。因此，如何分析负荷波动变化原因，实现负荷变化量化归因是一个具有实践应用价值的工作。

来源：《中国电力》2024年第8期

引文：邱敏, 周颖, 赵伟博, 等. 基于特征构建的区域电力负荷增长归因及量化分析方法[J]. 中国电力, 2024, 57(8): 190-205.

《中国电力》2024年第8期刊发了邱敏等撰写的《基于特征构建的区域电力负荷增长归因及量化分析方法》一文。文章基于区域级电力电量数据，从特征构建的角度，提出了一种区域电力负荷增长归因及量化分析方法。首先，利用鱼骨图定性分析影响电力负荷增长的各种因素，确定负荷增长归因及量化分析方法的研究思路；其次，从数据驱动的角度，构建能够表征气象因素、经济因素和特殊事件的相关指标；然后，对负荷进行分解，提取气象负荷、自然经济负荷、业扩负荷、随机负荷，利用不同负荷增长对总负荷增长的贡献率来定量表征其对负荷增长的影响程度；最后，基于上述电力负荷增长归因及量化分析方法构建负荷增长分析模型，并利用西北某2省的电力营销数据进行算例分析，验证该分析模型的有效性。

摘要

电力负荷由于受到气温、经济、特殊事件等多种因素及多因素耦合影响，增长成因量化分析困难。同时，目前对于电力负荷研究多集中于预测方面，对负荷增长原因分析较少。通过研究电力负荷数据特征构建方法，提出一种电力负荷增长归因分析方法。首先，构建气象相关性指标、基于经济发展的自然负荷增长指标、基于电力电量修正的产业结构变化指标以及事件趋势一致性评价指标；在此基础上，分别提取气象负荷、自然经济负荷、业扩负荷、随机负荷，利用贡献率量化各因素对负荷增长的影响程度。最后，利用西北某2省的电力电量数据进行验证，结果显示所提方法能够很好地量化负荷增长的原因。

01

负荷增长归因及量化分析研究思路

电力负荷一般可分为受气象影响的气象负荷、受社会经济发展的基础负荷和受休息日或特殊事件影响的随机负荷，即

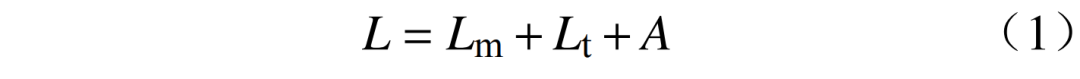
式中：L为总用电负荷；Lm为受气象因素影响的季节性波动负荷，主要指夏季由空调等降温设备产生的降温负荷和冬季的电采暖负荷；Lt为基础负荷，受社会经济发展等因素影响，也称为趋势负荷、经济负荷；A为受休息日或特殊事件影响的随机负荷。气温因素、经济因素与特殊事件对总负荷变化影响如图1所示。

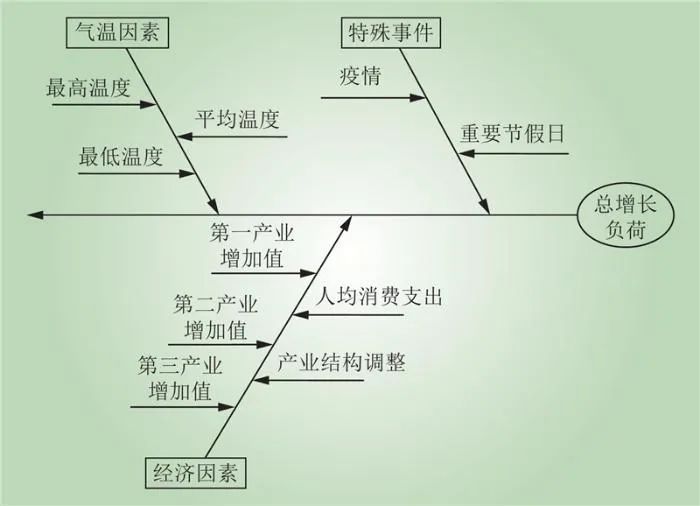
图1  总负荷变化影响因素

Fig.1  Influencing factors of total load change

在图1中，气温主要考虑最高温度、最低温度与平均温度。经济因素主要考虑产业结构调整、三次产业的增加值与人均消费支出，后两者均可在政府官网中查询，特殊事件主要考虑疫情、重要节假日以及常见的周末休息等。

本文提出了负荷增长的量化分析方法，基于气象负荷、基础负荷和随机负荷，分别构建相应的数据指标，定量表征气温、经济、特殊事件3种因素对于负荷变化的影响程度。该负荷增长量化分析研究思路如图2所示。基于负荷增长原因定性分析，从数据驱动的角度，构建能够表征这些影响因素的数据指标，主要包括气象相关性指标、基于经济发展的自然负荷增长指标、基于电力电量修正的产业结构变化指标、事件趋势一致性评价指标；基于这些指标对总负荷进行分解后，利用分负荷对总负荷的贡献率来定量表征其对负荷增长的影响程度。

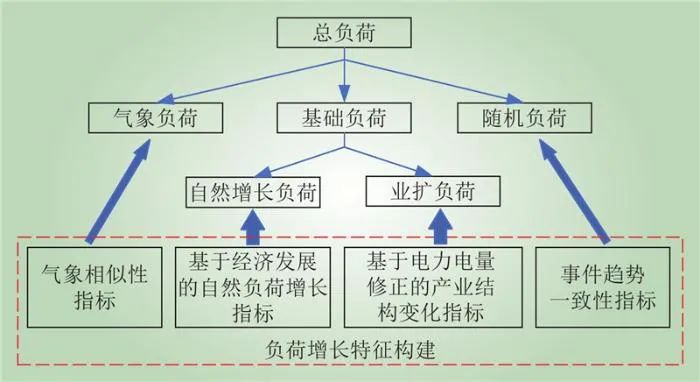
图2  基于特征构建的负荷增长量化分析研究思路

Fig.2  Research frame for quantitative analysis of load growth based on feature construction

02

基于特征构建的负荷增长量化分析

基于上述负荷增长归因及量化分析方法的研究思路，构建负荷增长量化分析模型。该模型量化分析气象、经济、特殊事件3种因素对负荷增长的影响，通过贡献率指标反映每种因素的影响程度。

由式（1）可知，负荷增长变化量可表示为

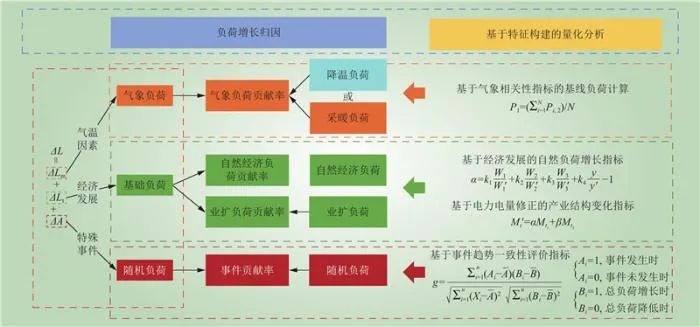
图3  负荷增长量化分析模型架构

Fig.3  Architecture of load growth quantitative analysis model

2.1  负荷增长特征构建

2.1.1  特征构建

特征构建需要从原始数据中人为地构建新的特征，这需要大量时间去研究真实的数据样本，思考负荷增长这一问题在电力大数据中的潜在形式，并将其更好地应用于负荷增长分析模型中。通过洞察和分析，对原始电力大数据进行精细特征构建，提取一系列具有物理意义的相关特征指标，辅助负荷增长分析模型获得更好的效果。

2.1.2  气象相关性指标

气象因素主要包括气温、湿度、降雨量等，一般可通过相关性分析来确定气象因素与负荷的相关性，从而排除相关性较小的因素，简化分析过程。常用的相关性方法为皮尔逊相关系数法，通过计算变量直接的皮尔逊相关系数大小，从而确定变量之间的相关性强弱。皮尔逊相关系数r为

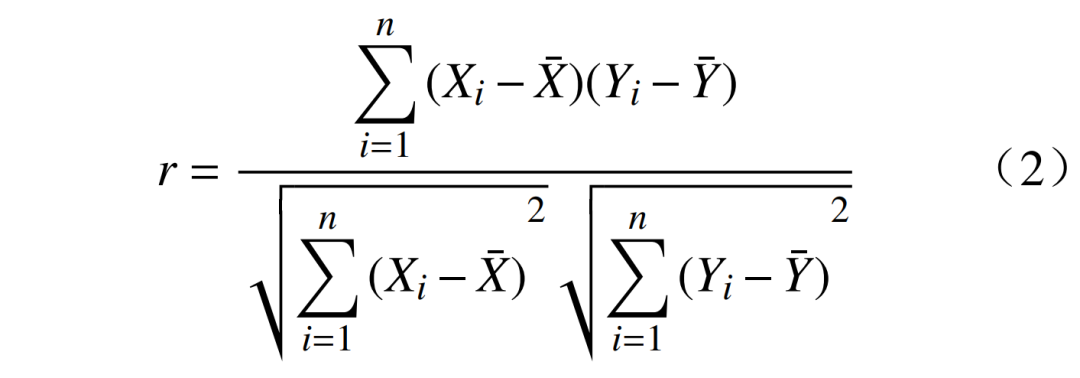
式中：Xi为变量1第i个样本数据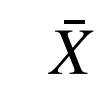；为变量1的样本平均值；Yi为变量2第i个样本数据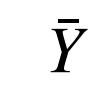；为变量2的样本平均值；n为样本数据个数。

考虑到各气象因素在不同时间存在着不同特性，具有一定的时域特性，对负荷影响程度会发生改变。如在7、8月份高温天气下，空调等降温设备的大量使用会增加电力系统的负荷峰值；在1、2月份寒冷天气下，电采暖等采暖设备的使用量巨大，同样会对电力负荷产生影响；而4、5月份天气凉爽，降温、采暖设备使用率低，对负荷影响小。因此，本文以月为单位，将分析时段隔开，分别计算每段时间内负荷与各气象因素的相关性指标，从而分析各气象因素时域特性对负荷的影响。

2.1.3  基于经济发展的自然负荷增长指标

经济因素是影响电力负荷的另一个重要因素，主要包括国家经济、工业、交通、商业、农业等领域的发展状况以及居民生活水平、用电需求等方面，其对于电力负荷的影响主要体现在基础负荷中。同时，业扩报装作为经济因素的重要体现，在负荷分析中不可忽略，这里将基础负荷分解为自然经济负荷和业扩负荷，分别研究二者对于负荷变化的影响。

自然经济负荷主要指除去业扩报装影响外，受到经济发展影响的负荷，其增长相对稳定。产业增加值和人均消费支出分别作为反映产业发展情况和生活水平的指标，能够在一定程度上反映电力电量的需求情况，因而可使用这些指标去拟合自然经济负荷的变化趋势。本文提出了一种基于经济发展的自然经济负荷变化趋势分析方法，利用产业增加值和人均消费支出推导而来的增长指标对自然经济负荷的增长情况进行表征。基于经济发展的自然负荷增长指标a为

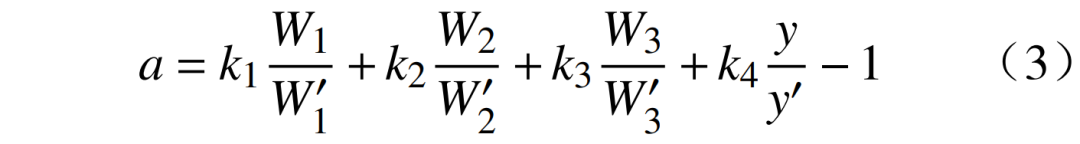
式中：k1、k2、k3、k4分别为第一产业、第二产业、第三产业、城乡居民的用电量占比；W1、W2、W3分别为第一、二、三产业分析期当季产业增加值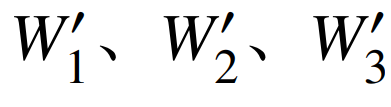；分别为第一、二、三产业基准期季度产业增加值；y为分析期人均消费支出；为基准期人均消费支出。

需要注意的是，当用于分析仅相差1个季度时段时（如2季度与1季度），人均消费支出取人均消费支出季度值；当用于分析相差2个及以上季度的时段时（如3季度和1季度），人均消费支出取人均消费支出累计值。

2.1.4  基于电力电量修正的产业结构变化指标

产业结构是指农业、工业和服务业在一国经济结构中所占的比重，也是体现发展中国家和发达国家之间经济发展差距的一个重要指标，合理的产业结构是后发国家赶超先发国家，加快经济发展的必然要求。改革开放之初，中国东部地区依靠自身地理优势，凭借着特殊的政策优势，积极承接发达国家产业转移，产业结构逐步优化，经济得到迅速发展。但由于缺少承接产业转移经验，这种粗放式的承接产业转移导致东部沿海地区出现产业过度聚焦和环境污染问题。相对于东部沿海地区，中国中西部地区有着资源与劳动力的比较成本优势，随着中西部地区基础设施完善，中西部地区逐渐成为承接产业转移的首选地区。因此，在分析区域尤其是中西部地区的电力负荷变化时，需要考虑产业转移带来的产业结构变化影响。

传统的产业结构变化指标为Moore指标，可用于反映产业结构变化快慢，其计算式为

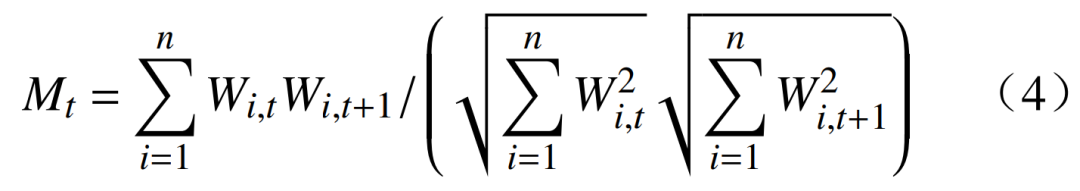
式中：Mt为t期Moore产业结构变化值；Wi,t为t期第i产业所占比重。

在传统产业结构变化Moore指标的基础上，本文提出一种基于电力电量修正的产业结构变化指标。将式（4）中经济数据替换为产业负荷数据，考虑到负荷数据是瞬时值而经济数据是累积值，进一步引入电量进行修正，对负荷与电量分别给予权值，避免瞬时负荷数据引起较大误差。基于电力电量修正的产业结构变化指标为

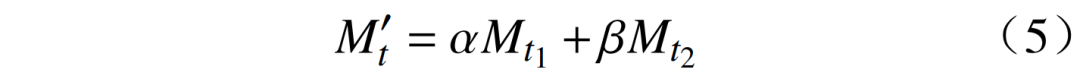
式中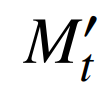：为t期Moore产业结构变化指数；α为电量系数；β为负荷系数，α和β取值受对负荷和电量关注程度的影响，取值范围为0~1，可结合实际应用场景由专家经验确定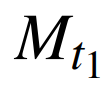；为t期Moore电量结构变化指数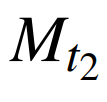；为t期Moore负荷结构变化指数。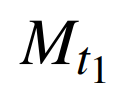计算式为

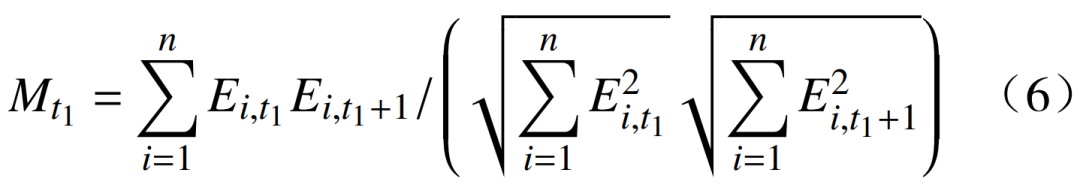
式中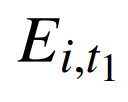：为t期（基准期）第i产业电量所占比重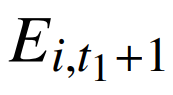；为t+1期（分析期）第i产业电量所占比重。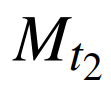计算方法与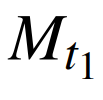一致，相应数据改为负荷数据即可。

该指标与传统的Moore指标类似，均是以向量空间中夹角为基础，将2个时期内2组向量间的夹角作为表示产业结构变化程度的指标。因此，在表征产业结构变化程度时，须对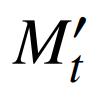进行反余弦变换以得到夹角值。

定义产业之间变化的Moore夹角θ为

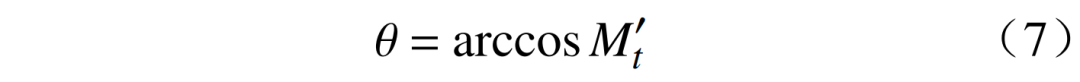
该Moore夹角越大，说明产业结构变化速率越大。

2.1.5  事件趋势一致性评价指标

对于一些特殊事件，如疫情、重大活动（如奥运会等）、重要节假日（如国庆、春节等）以及常见的周末休息等事件，对于负荷变化的影响往往不可忽略。这些事件往往是抽象的，难以进行量化，因此其是否对负荷变化产生影响常常是通过专家经验进行判断，存在很大的误差。本文提出一种事件趋势一致性评价指标，用来分析事件与负荷变化的相关程度，具体方法如下。

以自然日为单位，构建2个时间序列A、B，并进行标幺化处理，即当第i个自然日为事件发生日时Ai置1，否则置0；当第i个自然日总负荷增长时Bi置1，降低时置0。利用式（2）中的皮尔逊相关系数r计算A、B数据之间的相关性，r越大，说明该事件对负荷变化的影响越大。事件趋势一致性评价指标g为

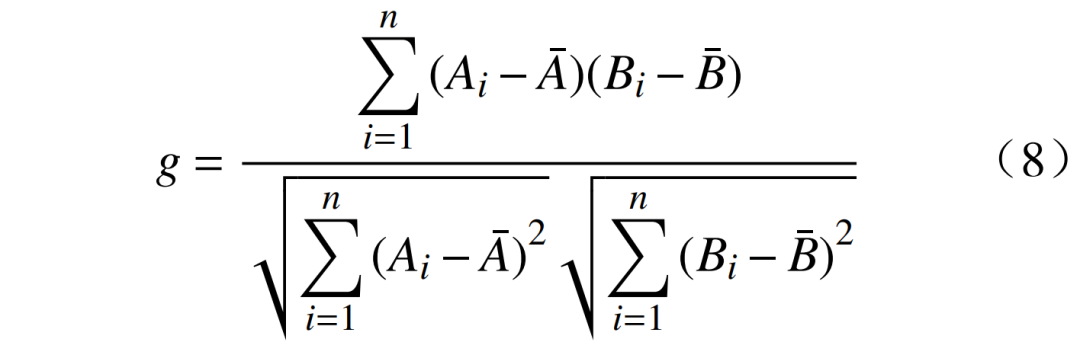
i的取值视特殊事件持续时间设定，g的取值范围为[?1,1]。参考皮尔逊相关系数的性质，衡量该事件对负荷变化的影响程度时有：0＜|g|＜0.4为低度线性相关；0.4?|g|＜0.7为显著线性相关；0.7?|g|＜1为高度线性相关。

2.2  基于特征构建的负荷分解

对负荷增长特征进行构建后，参照图2对总负荷按照影响因素进行分解，为定量分析不同影响因素对负荷增长的影响程度作数据准备。

2.2.1  基于气象相关性指标的气象负荷提取

气象负荷主要指夏季的空调降温负荷和冬季的电采暖负荷，该部分负荷常常难以直接计算，一般采用基准负荷比较法进行估算。

通常情况下春季和秋季不存在气象负荷或者气象负荷很小，因此可选取春季或秋季气象因素与负荷相关性低的日期为典型工作日，认定为该地区春季无降温负荷或秋季无采暖负荷的典型工作日，对典型工作日同一行业同一时刻的负荷数据进行平均，得到相应行业相应时刻下春季工作日基线负荷P1为

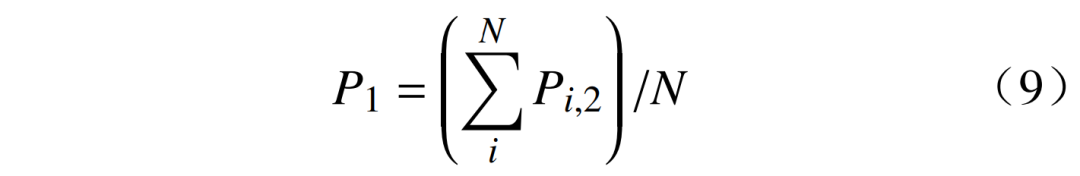
式中：Pi,2为第i天工作日的负荷；N为总天数。

同理，休息日基线负荷采用休息日的负荷进行计算即可，并通过分析期的实际负荷减去基线负荷即可得到对应的气象负荷Lm为

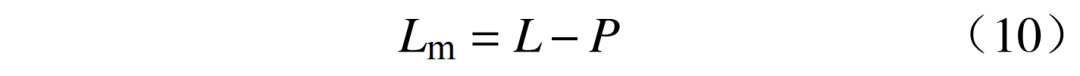
式中：L为总负荷；P为对应的工作日基线负荷或休息日基线负荷。

2.2.2  基于自然负荷增长指标的基础负荷

基础负荷可分为受经济发展影响的自然经济负荷和业扩报装所引起的新增负荷2部分。

自然经济负荷P2可根据基于经济发展的自然负荷增长指标a得到，即

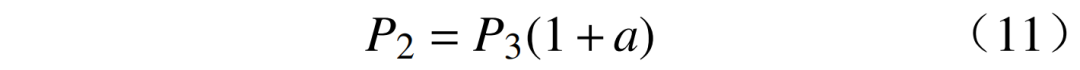
式中：P3为上一季度平均负荷。

业扩报装所产生的业扩负荷为已知数据，无须进行计算。

2.2.3  随机负荷

随机负荷主要指受休息日或特殊事件影响的负荷，该部分负荷通常被作为随机误差项进行处理。然而，实际上该部分负荷在重要节假日、疫情、极端天气等特殊事件的影响下，有时数值并非很小，因此在进行负荷分析时需要考虑该部分负荷。但由于该部分负荷具有随机性，需要通过计算发生事件时的总负荷与事件发生前的总负荷的差值进行估算，即

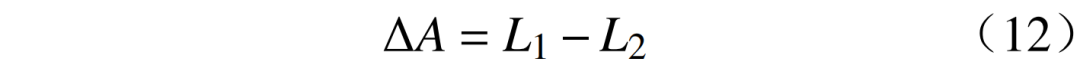
式中：A为事件引起的随机负荷变化值；L1为事件发生前的负荷；L2为发生该事件时的负荷。

2.3  量化归因

贡献率可用于表征在负荷增长过程中，各项分负荷的变化程度，从而体现出各类影响因素对于负荷增长的作用程度。该指标的核心思想为分量变化值/总变化值，可通过该指标的大小反映出气象、经济和特殊事件对于负荷增长的影响程度。在对总负荷完成分解之后，根据所得气象负荷、自然经济负荷、业扩负荷和随机负荷的变化值可得到对应的贡献率，从而定量分析气象、经济、特殊事件对于负荷增长的影响，对负荷增长进行量化归因。各类负荷的贡献率计算方法如下。

1）气象负荷贡献率η1为

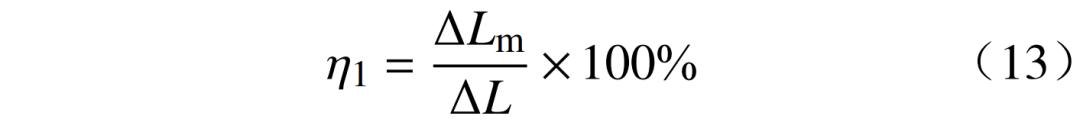
式中：L为气象负荷增加值；L为总负荷增加值。

2）自然经济负荷贡献率η2为

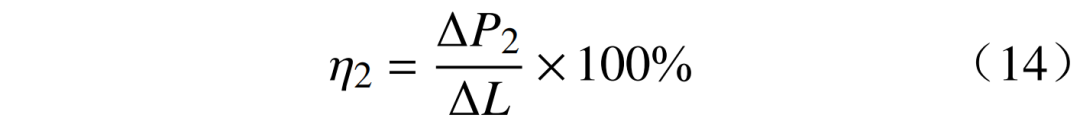
式中：P2为自然经济负荷增加值。

3）业扩负荷贡献率η3为

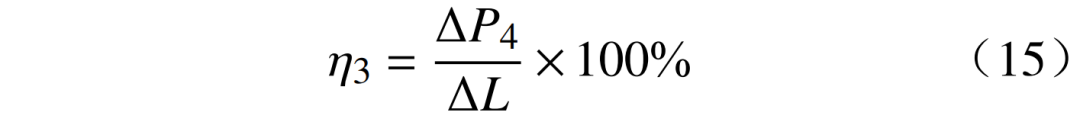
式中：P4为业扩负荷增加值。

4）随机负荷贡献率η4为

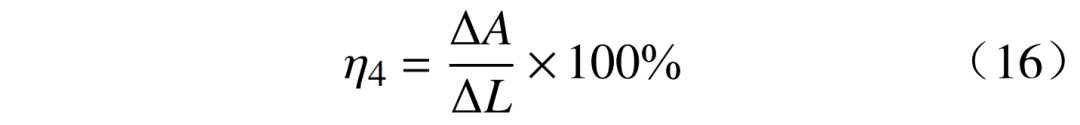
03

算例分析

3.1  数据说明

本文采用西北区域1、区域2实际收集的负荷数据和气象数据，对所提方法进行验证。其中，算例1分析时长为1个季度，用于验证本文所提方法在较短时段内的适用性。该算例负荷数据主要包括2022年区域1、区域2全年负荷数据；气象数据主要包括负荷数据相对应的日最高温度、最低温度、平均温度、平均风速等。考虑到气象负荷主要集中在夏季和冬季，而冬季往往存在跨年问题，因此选取4~7月初作为分析区间，以7月最大负荷发生时刻负荷增长归因为目标展开分析。算例2分析时长为3年，用于验证本文所提方法在较长时段内的适用性。该算例负荷数据主要包括2020年至2023年7月区域1负荷数据，气象数据维度与算例1相同，以2023年7月最大负荷发生时刻的负荷增长归因为目标展开分析。结合实际数据对本文构建的负荷增长特征指标进行算例分析，基于这些指标对总负荷进行分解后，利用贡献率明确各因素对负荷增长的影响程度。

3.2  算例1

3.2.1  基于气象相关性指标的气象负荷计算

不同月份气象因素与负荷的相关性存在较大差异，这里通过计算最高温度、最低温度、平均温度、平均风速4个气象因素与负荷的相关性，分析相关性的时域特性，从而确定气象负荷的基线负荷选取日期，并计算气象负荷数值。具体流程如图4所示。

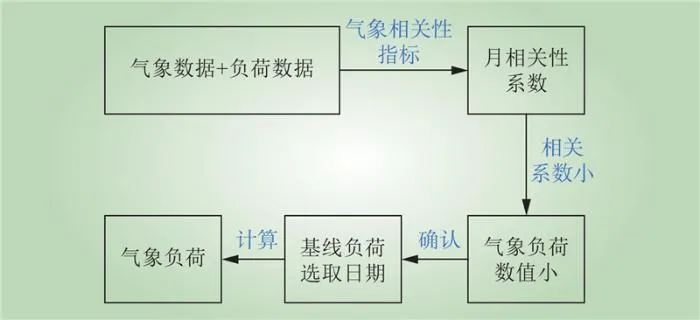
图4  基于气象相关性指标的气象负荷分析流程

Fig.4  Flow chart of meteorological load analysis based on meteorological correlation index

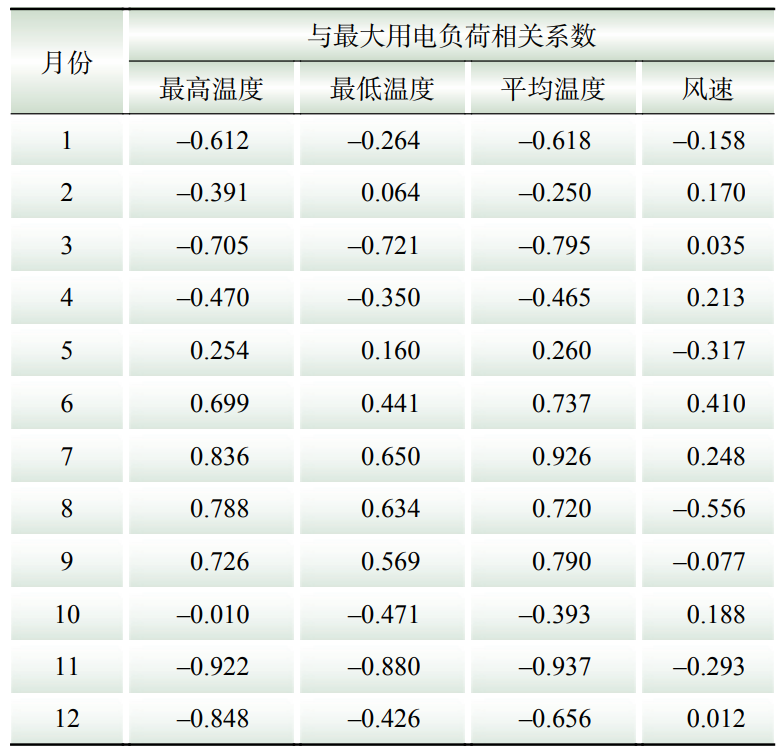
1）区域1气象负荷计算。区域1最大用电负荷与4个因素的相关性如表1所示。

表1  2022年区域1气象因素与最大用电负荷相关性

Table 1  Correlation between meteorological factors and maximum electricity load in area 1 in 2022

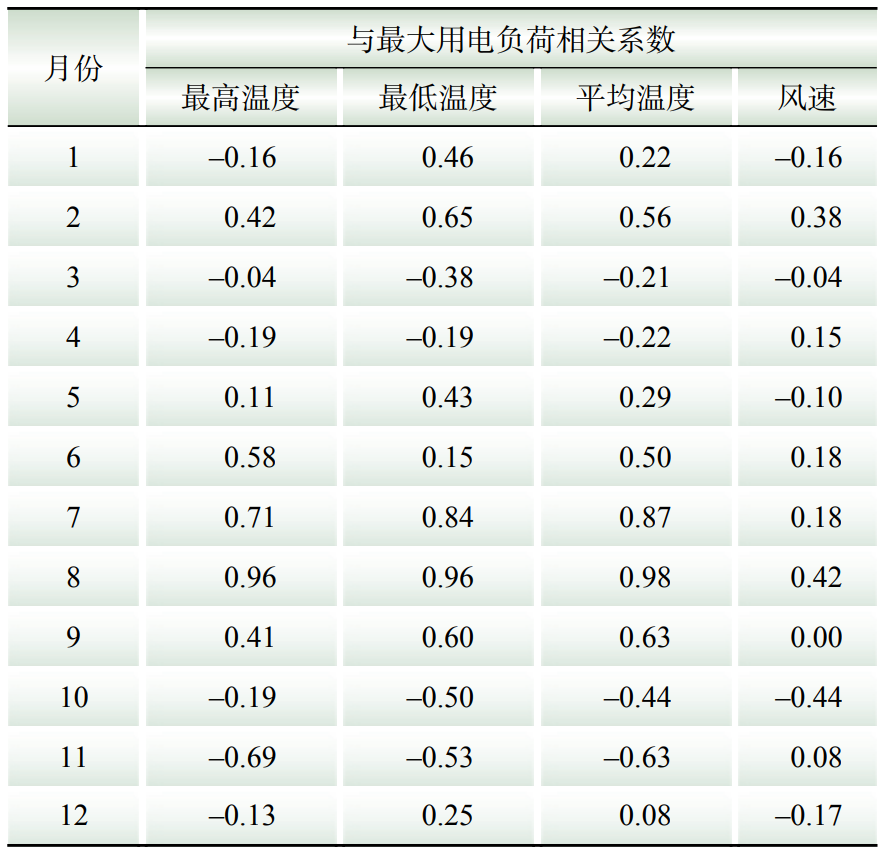
根据表1，风速与负荷之间相关性弱，可忽略；温度与负荷相关性存在明显时域特性。7月和8月相关性较其他月份更加显著，表明这2个月气象负荷数值大，对总负荷作用显著。3月和4月气象相关系数均偏低，表明这2个月气象负荷数值小。根据2.2.1节，结合季节因素，选择4月作为基线负荷选取日期。

根据式（9）可得，2022年区域1工作日全社会用电负荷、第一产业、第二产业、第三产业以及居民用电基线负荷如图5所示。

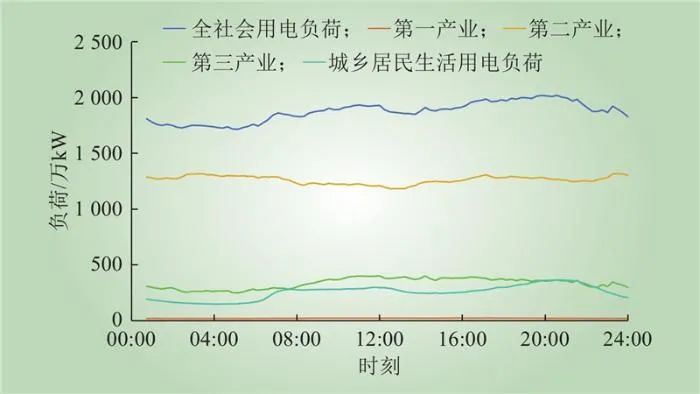
图5  2022年区域1工作日基线负荷曲线

Fig.5  Baseline load curves of working days in area 1 in 2022

2022年区域1休息日全社会用电负荷、第一产业、第二产业、第三产业以及居民用电基线负荷如图6所示。

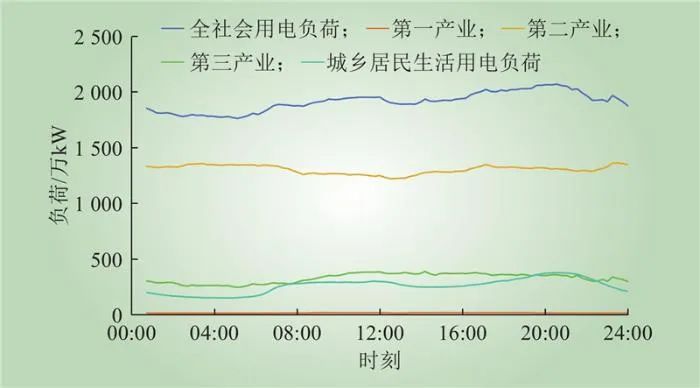
图6  2022年区域1休息日基线负荷曲线

Fig.6  Baseline load curves of holidays in area 1 in 2022

4月份区域1最大负荷时刻为2022-04-02 T19:45，7月份最大负荷时刻为2022-07-09 T16:45，负荷增长万kW，根据式（10）与图6可得2022-07-09 T16:45时的气象负荷增长Lm为820.52万kW。

2）区域2气象负荷计算。区域2最大用电负荷与4个气象因素的相关性如表2所示。

表2  2022年区域2气象因素与最大用电负荷相关性

Table 2  Correlation between meteorological factors and maximum electricity load in area 2 in 2022

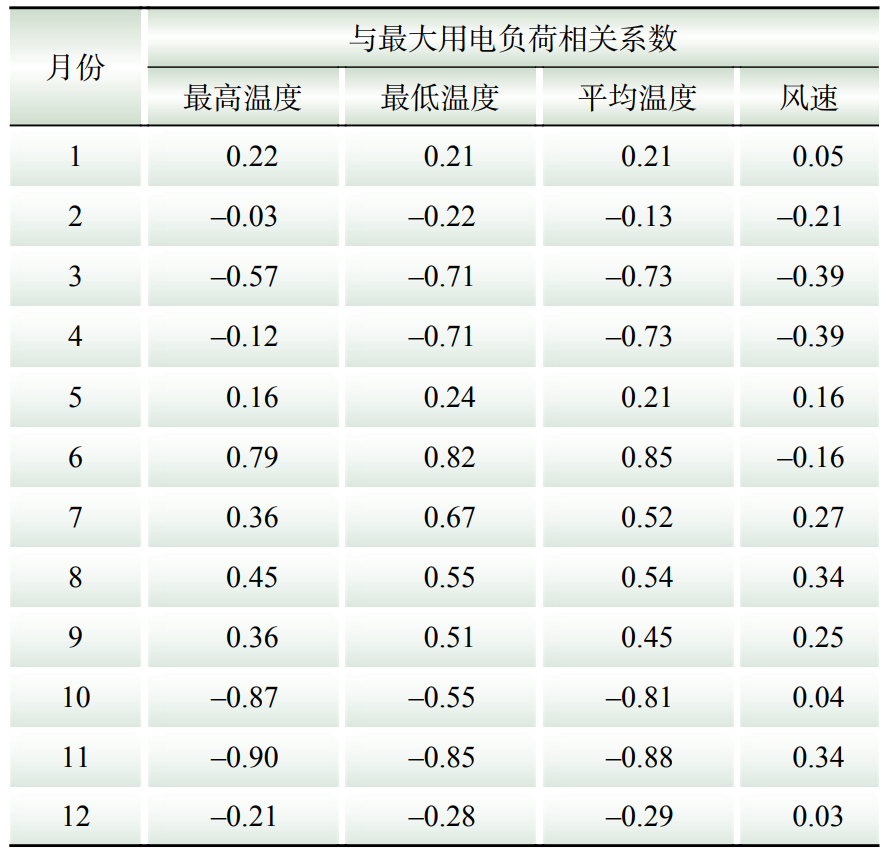
根据表2，区域2风速与负荷之间的相关性同样较弱，可忽略；温度与负荷相关性存在明显的时域特性。3、4、6、7、10和11月等跨季节月份相关性较其他月份更加显著，表明区域2负荷受气象因素影响较强。其中，5月气象相关系数均偏低，表明该月气象负荷数值小。根据2.2.1节，结合季节因素，选择5月作为基线负荷选取日期。

根据式（9）可得，2022年区域2工作日全社会用电负荷、第一产业、第二产业、第三产业以及居民用电基线负荷如图7所示。

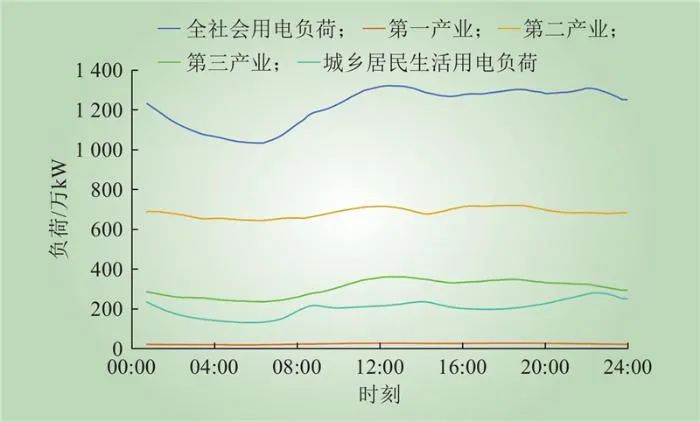
图7  2022年区域2工作日基线负荷曲线

Fig.7  Baseline load curves of working days in area 2 in 2022

2022年休息日区域2全社会用电负荷、第一产业、第二产业、第三产业以及居民用电基线负荷如图8所示。

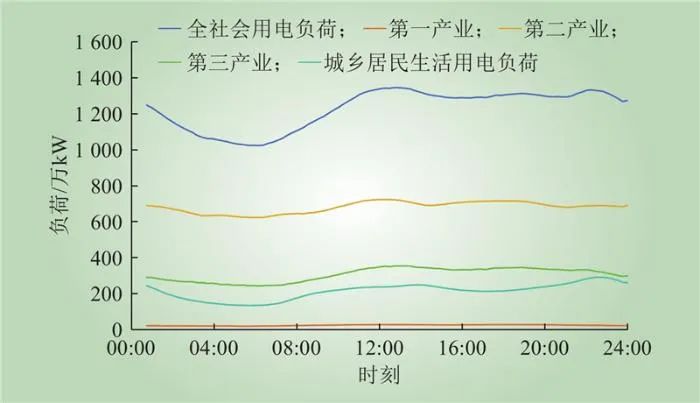
图8  2022年区域2休息日基线负荷曲线

Fig.8  Baseline load curves of holidays in area 2 in 2022

4月份区域2最大负荷时刻为2022-04-01 T20:15，7月份最大负荷时刻为2022-07-01 T16:15，负荷增长610.33万kW，根据式（10）与图7可得2022-07-01 T16:15时的气象负荷增长Lm为504.76万kW。

3.2.2  自然经济负荷增长分析

基于省政府及国家统计局公布的经济指标数据，分别计算区域1和区域2的自然经济负荷增长指标，并提取总负荷增长量中的自然经济负荷增长分量。

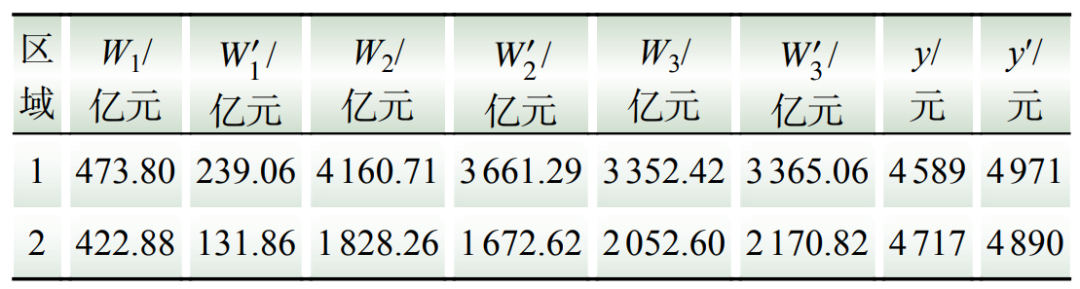
由于分析区间为4月至7月初，可看作2022年1季度与2季度。2.1.3节中式（3）所用数据如表3所示。

表3  2022年区域1与区域2第1、2季度三次产业的产业增加值与人均消费支出情况

Table 3  Industrial added value and per capita consumption expenditure of the third industry in the first and second quarters of area 1 and area 2 in 2022

1）区域1自然经济负荷增长量。区域1第一产业用电量占比为0.36%，第二产业用电量占比为63.03%，第三产业用电量占比为22.10%，城乡居民用电占比为14.51%，可得自然增长指标a为7.75%。因此，区域1自然经济负荷增长量可由式（11）推导得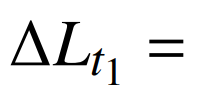1804.17×7.75%=139.91万kW。

2）区域2自然经济负荷增长量。区域2第一产业用电量占比为2.36%，第二产业用电量占比为52.06%，第三产业用电量占比为30.43%，城乡居民用电占比为15.15%，可得自然增长指标a为7.86%。因此，区域2自然经济负荷增长量可由式（11）推导得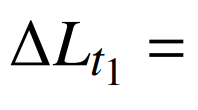1317.47×7.86%=103.59万kW。

3.2.3  产业结构变化分析

考虑到产业结构变化一般时间较长，这里将分析时段选为2022年1月至2022年7月初。以式（5）中α和β均取0.5为例，实际运用时可根据对负荷和电量的重视程度给予合适权重。

1）区域1产业结构变化分析。根据2.1.4节，区域1产业结构变化值夹角θ如图9所示。可以看出，区域1产业结构夹角值在2左右波动，但在5月份产业结构出现明显变化，产业结构变化值接近6。

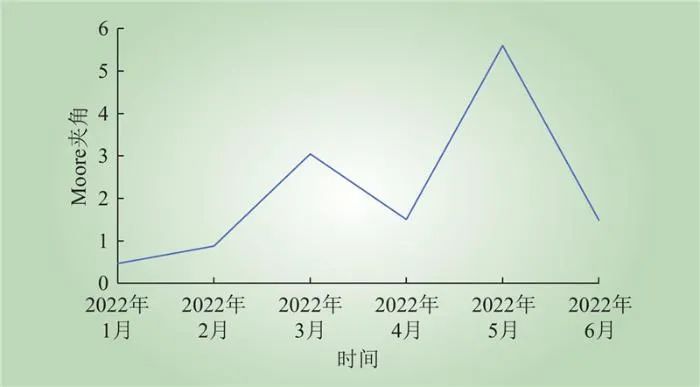
图9  区域1产业结构变化值夹角变化趋势

Fig.9  The change trend of the included angle of industrial structure change value in region 1

结合实际数据，区域1各产业的变化情况如图10所示。5月份该区域第二产业最大负荷占比下降近7%，引起产业结构发生变化。

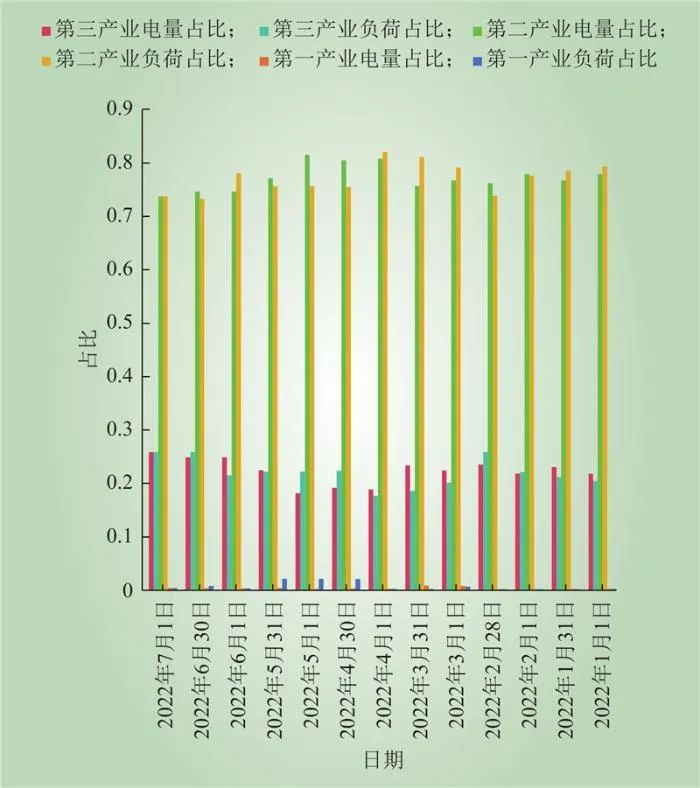
图10  2022年1—7月区域1负荷与电量占比变化情况

Fig.10  Changes in the proportion of load and electricity in area 1 from January to July 2022

2）区域2产业结构变化分析。根据2.1.4节，区域2产业结构变化值夹角θ如图11所示。可以看出，区域2产业结构夹角值在2左右波动，但在3月份和6月份产业结构出现明显变化。

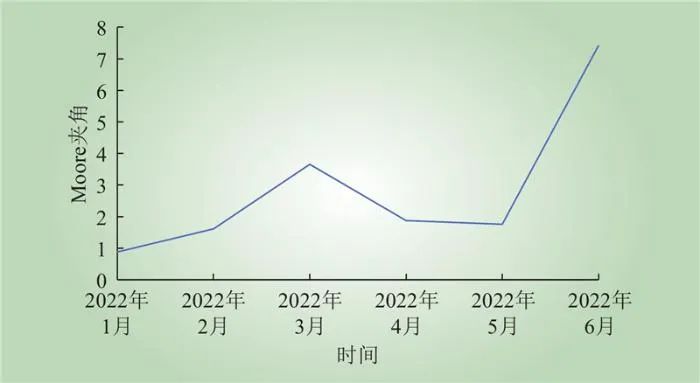
图11  区域2产业结构变化值夹角变化趋势

Fig.11  The change trend of the included angle of industrial structure change value in area 2

结合实际数据，区域2各产业的变化情况如图12所示。3月该区域第二产业最大负荷占比上升近4%，6月该区域第二产业电量占比下降近7%，引起产业结构发生变化。

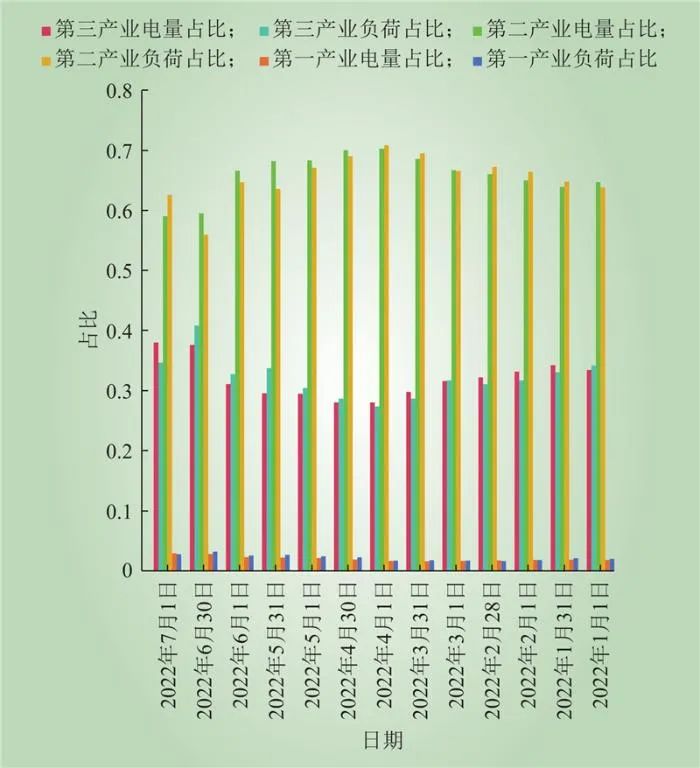
图12  2022年1—7月区域2负荷与电量占比变化情况

Fig.12  Changes in the proportion of load and electricity in area 2 from January to July 2022

由区域1和区域2产业结构变化情况分析可以验证，本文提出的产业结构变化指标能够从电量和负荷2方面对产业结构变化进行刻画，指标对产业结构变化的敏感性较高。

3.2.4  事件趋势一致性评价分析

分析期与基准期均位于疫情期间，且无重大活动或极端天气发生，这里仅考虑休息日的影响。通过式（8）获取表征事件发生和负荷变化的2个时间序列A、B后，计算序列A与序列B的相关系数结果如表4所示。

表4  休息日与日负荷增长g值

Table 4  The correlation value g between holidays and daily load growth

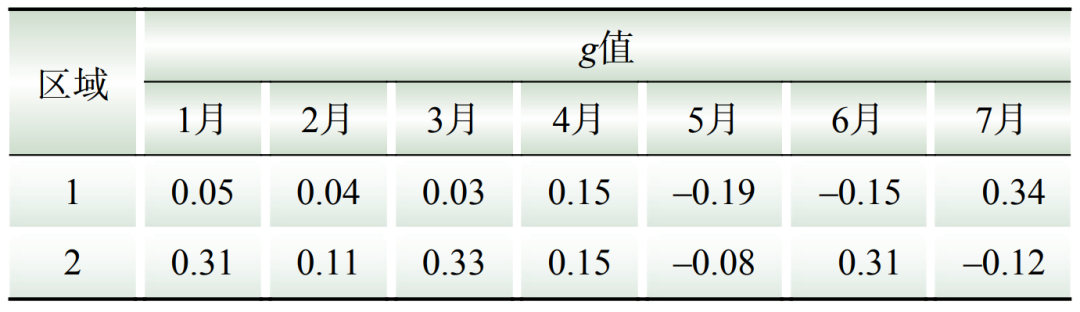
根据表4，区域1用电负荷与休息日相关系数绝对值普遍低于0.4，相关性较弱。但在2月和6月相关系数绝对值大于0.4，呈现出显著相关性。同样地，区域2用电负荷与休息日相关系数绝对值普遍低于0.4，相关性较弱，但在1月、3月、6月度冬/度夏期间相关性系数相较于其他月份同样偏高。结合经验分析，一般2月份采暖负荷逐渐减少，6月降温负荷逐渐增长，表明休息日对于气象负荷存在一定影响。

3.2.5  负荷增长量化归因

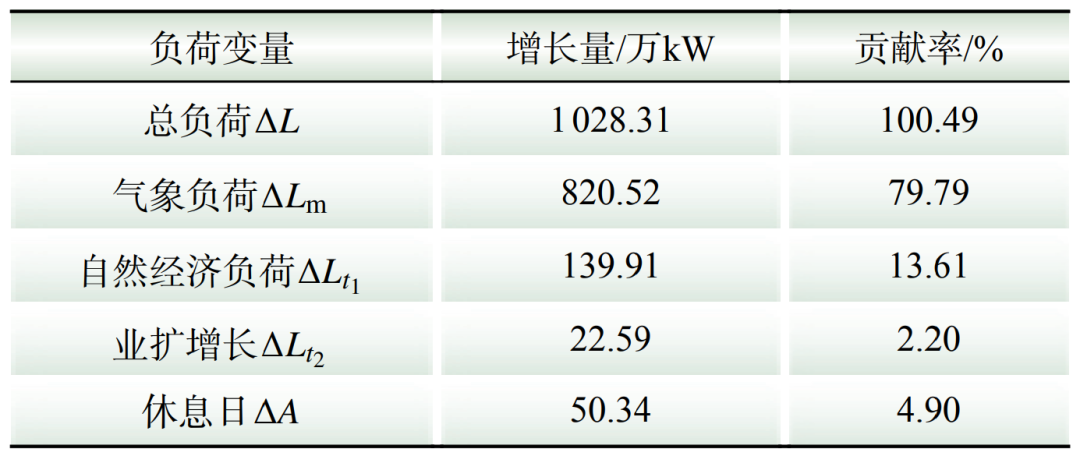
1）区域1负荷增长量化归因。根据3.2节可知，区域1在所选取的分析区段内最大负荷发生在7月9日，增长量L=1028.31万kW，气象负荷增长L=820.52万kW，自然经济负荷增长量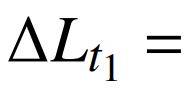139.91万kW。对于业扩负荷，7月与4月区域1业扩负荷差值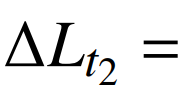22.59万kW。考虑休息日的影响，由于7月9日为周六，根据式（12）可得休息日引起的负荷增长A=50.34万kW。因此，计算基于贡献率的区域1负荷增长量化归因情况如表5所示。

表5  基于贡献率的区域1负荷增长量化归因情况

Table 5  Quantitative attribution of load growth in area 1 based on contribution rate

2）区域2负荷增长量化归因。根据3.2节可知，区域2在所选取的分析区段内最大负荷发生在7月1日，增长量L=610.33万kW，气象负荷增长L=504.76万kW，自然经济负荷增长量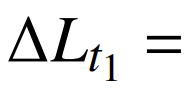103.59万kW。对于业扩负荷，7月与4月区域2业扩负荷差值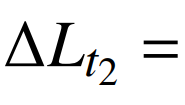7.77万kW。考虑休息日的影响，7月1日为周五，无休息日影响，即A=0。因此，计算基于贡献率的区域2负荷增长量化归因情况如表6所示。

表6  基于贡献率的区域2负荷增长量化归因情况

Table 6  Quantitative attribution of load growth in area 2 based on contribution rate

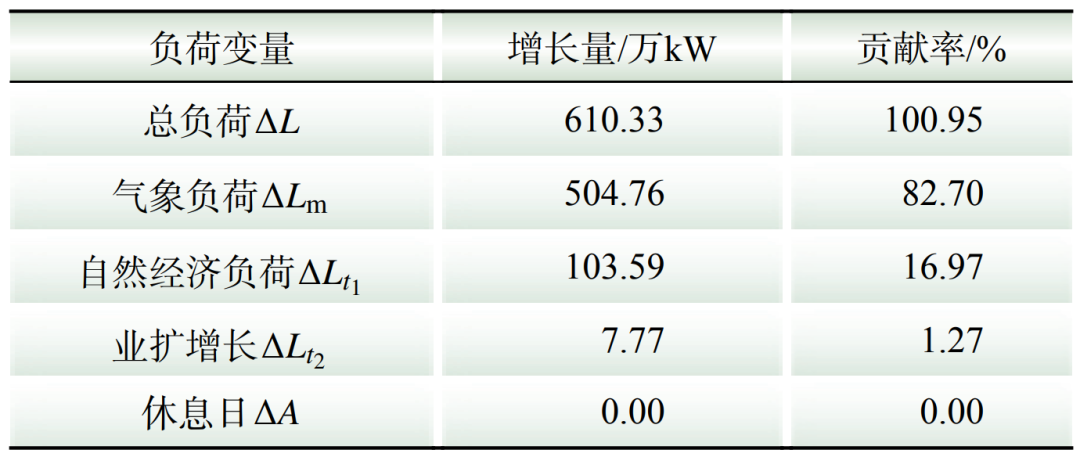
虽然各类负荷贡献率之和与理论值100%有所不同，但其差值在可接受范围之内，该问题主要由于各类负荷解耦不充分，仍存在一定交叉，如业扩报装产生的负荷与气象负荷、自然经济负荷均可能存在重叠部分，自然经济负荷与气象负荷也可能存在重叠部分等。

在表5和表6中，区域1和区域2负荷增长的主要原因均是气象负荷增长显著，即气象因素是引起区域1和区域2负荷增长的主要因素。由于分析区段位于夏季，天气炎热，空调等气象负荷增长显著，该分析结论符合客观事实，从而验证了本文所提负荷增长分析模型的有效性。

3.3  算例2

3.3.1  气象负荷变化分析

不同于算例1，算例2分析周期延伸至3年，从长期负荷分析角度对本文方法进行验证。本算例分析目标为2020年7月区域1最大负荷（即2020-07-09 T16:15）至2023年7月最大负荷（即2023-07-12 T13:15）增长量化归因。所选时期均位于夏季，故须分别计算2个时期的气象负荷。

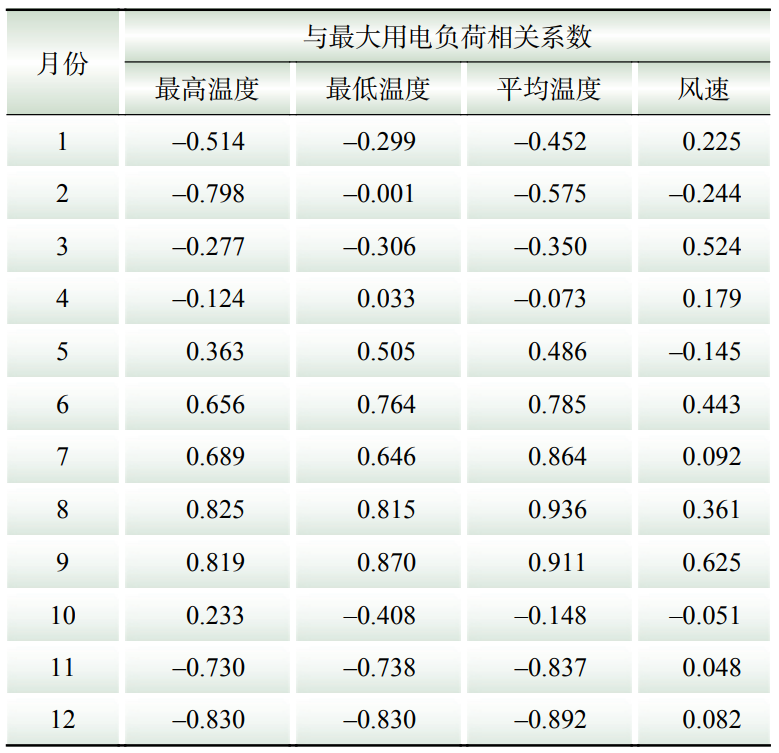
1）2020年区域1气象负荷计算。2020年区域1负荷与气象因素相关性情况如表7所示。

表7  2020年区域1气象因素与最大用电负荷相关性

Table 7  Correlation between meteorological factors and maximum electricity load in area 1 in 2020

根据表7，2020年5月区域1各气象指标与负荷相关系数均偏低，表明该月气象负荷数值小。根据2.2.1节，结合季节因素，可选择5月作为基线负荷选取日期。

根据式（9）可得，2020年区域1工作日全社会用电负荷、第一产业、第二产业、第三产业以及居民用电基线负荷如图13所示。

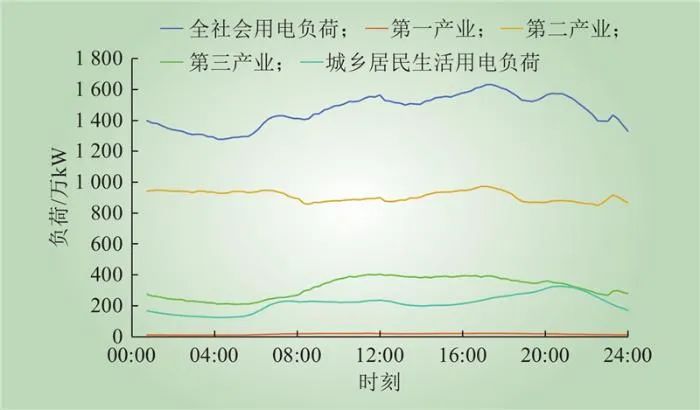
图13  2020年区域1工作日基线负荷曲线

Fig.13  Baseline load curves of working days in area 1 in 2020

2020年休息日区域1全社会用电负荷、第一产业、第二产业、第三产业以及居民用电基线负荷如图14所示。

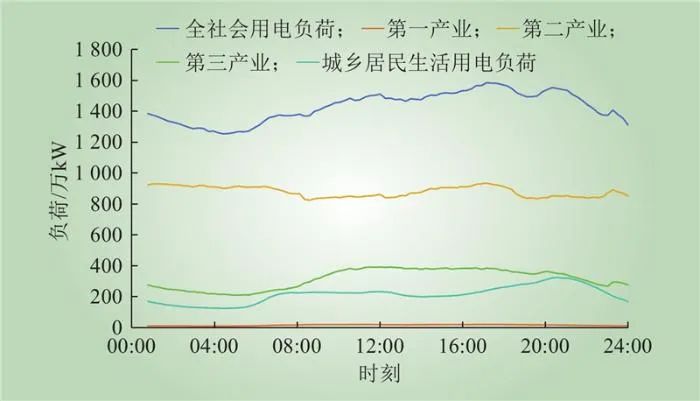
图14  2020年区域1休息日基线负荷曲线

Fig.14  Baseline load curves of holidays in area 1 in 2020

2020年7月区域1最大负荷时刻为7月9日16:15，根据式（10）与图13可得7月9日16:15气象负荷Lm=556.12万kW。

2）2023年区域1气象负荷计算。2023年区域1负荷与气象因素相关性情况如表8所示。

表8  2023年区域1气象因素与最大用电负荷相关性

Table 8  Correlation between meteorological factors and maximum electricity load in area 1 in 2023

根据表8，2023年4月区域1各气象指标与负荷相关系数均偏低，表明该月气象负荷数值小。根据2.2.1节，结合季节因素，可选择4月作为基线负荷选取日期。

根据式（9）可得，2023年区域1工作日全社会用电负荷、第一产业、第二产业、第三产业以及居民用电基线负荷如图15所示。

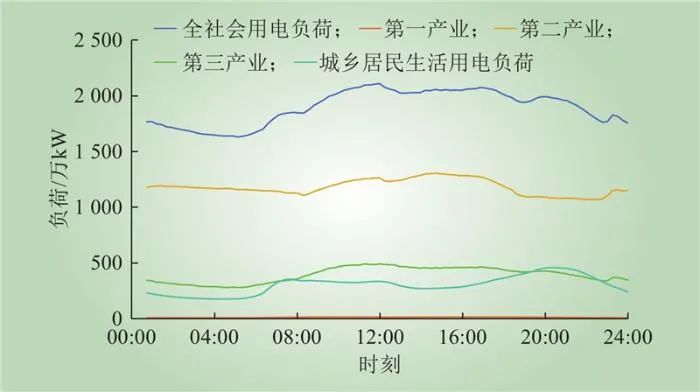
图15  2023年区域1工作日基线负荷曲线

Fig.15  Baseline load curves of working days in area 1 in 2023

2023年休息日区域1全社会用电负荷、第一产业、第二产业、第三产业以及居民用电基线负荷如图16所示。

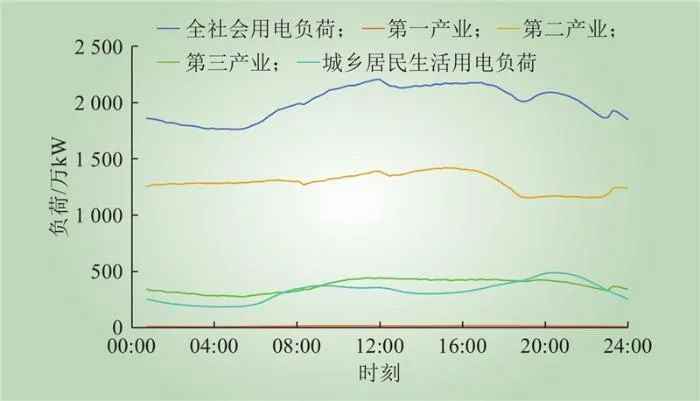
图16  2023年区域1休息日基线负荷曲线

Fig.16  Baseline load curves of holidays in area 1 in 2023

2023年7月区域1最大负荷时刻为7月12日13:15，根据式（10）与图14可得7月9日16:15气象负荷Lm=万kW。因此，气象负荷增长L为万kW。

3.3.2  自然经济负荷变化分析

算例2经济数据获取途径与算例1相同。由于分析区间为2020年7月初至2023年7月初，可看作2020年2季度与2023年2季度。2.1.3节中式（3）所用数据如表9所示。

表9  2020年与2023年区域1第2季度三次产业的产业增加值与人均消费支出情况

Table 9  Industrial added value and per capita consumption expenditure of the third industries in the second quarters of area 1 in 2020 and 2023

区域1第一产业用电量占比为0.86%，第二产业用电量占比为56.50%，第三产业用电量占比为20.08%，城乡居民用电占比为22.56%，可得自然增长指标a为28.16%。因此，区域1自然经济负荷增长量可由式（11）推导得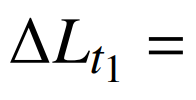1480.68×28.16%=417.03万。

3.3.3  长周期产业结构变化分析

由于算例2选取时间较长，这里以季度为组分析产业结构变化，式（5）中α和β均取0.5为例。

根据2.1.4节，区域1产业结构变化值夹角θ如图17所示。可以看出，区域1产业结构夹角值在2020年4季度至2021年1季度明显上升，在2021年2季度至3季度显著下降，而后逐渐趋于稳定。

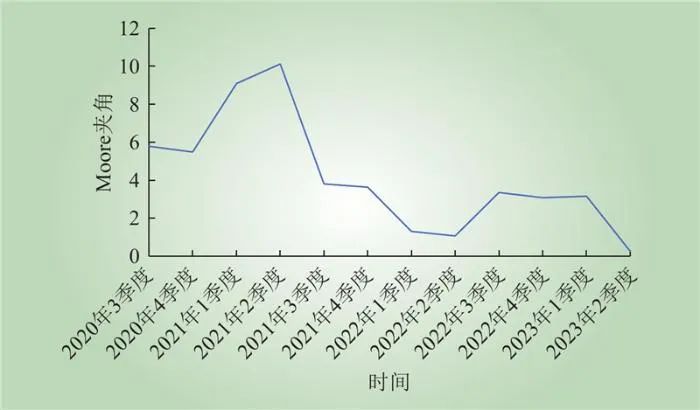
图17  区域1产业结构变化值夹角季度变化趋势

Fig.17  The quarterly change trend of the included angle of the industrial structure change value in the area 1

结合实际数据，区域1各产业的变化情况如图18所示，2020年4季度至2021年1季度该区域第三产业用电量占比下降超过5%，2021年2季度至2021年3季度该区域第三产业最大负荷占比下降近14%，引起产业结构发生变化。

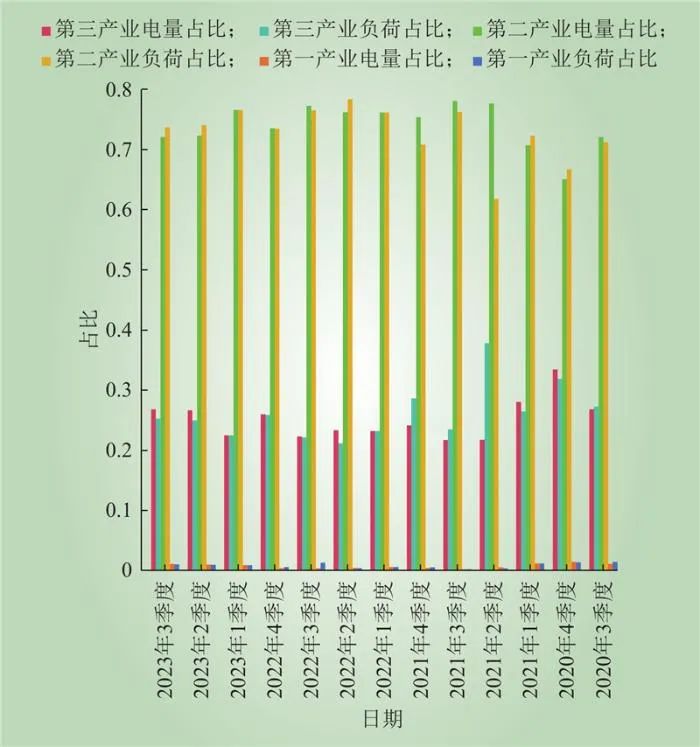
图18  2020年7月至2023年7月区域1负荷与电量占比变化情况

Fig.18  Changes in the proportion of load and electricity in area 1 from July 2020 to July 2023

3.3.4  长周期事件趋势一致性评价分析

分析期与基准期跨度较大，且无重大活动或极端天气发生，这里考虑以季度为组分析休息日的影响。通过式（8）获取表征事件发生和负荷变化的2个时间序列A、B后，计算序列A与序列B的相关系数结果如表10所示。

表10  2020年第3季度至2023年第2季度区域1休息日与日负荷增长g值

Table 10  The correlation value g between holidays and daily load growth from the second quarter of 2020 to the second quarter of 2023

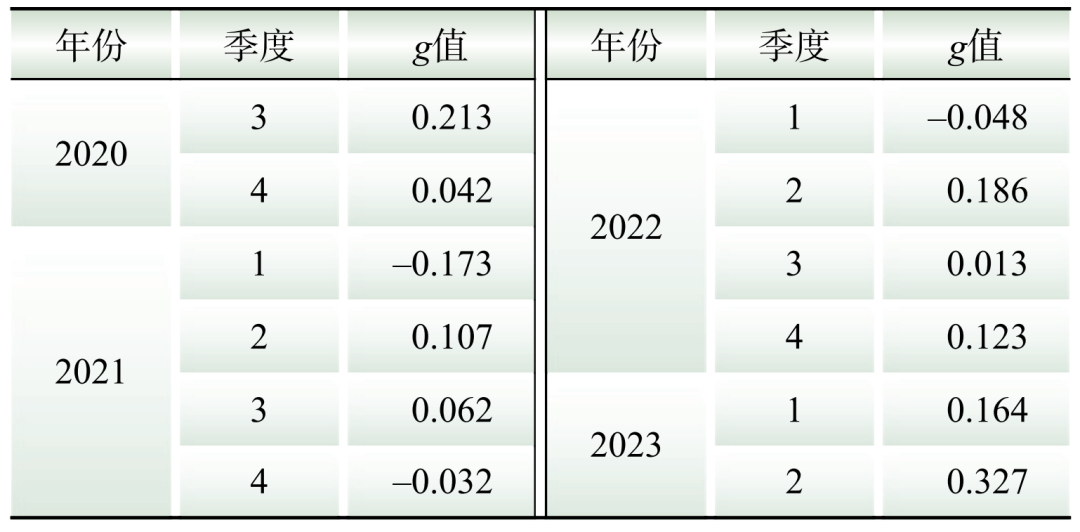
根据表10，区域1用电负荷与休息日相关系数绝对值普遍低于0.4，相关性较弱。但在2020年3季度和2023年2季度相关系数明显高于其他季度，推测可能是由于其他季度新冠疫情防控力度较这2个季度更为强力所导致。

3.3.5  负荷增长量化归因分析

根据3.2节可知，区域1在所选取的分析区段最大负荷增长量L=1441.58万kW，气象负荷增长L=1004.41万kW，自然经济负荷增长量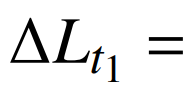417.03万kW。对于业扩负荷，由于数据限制，未获取该分析时段内业扩数据，暂取零处理，即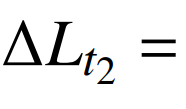0。考虑休息日的影响，由于2020年7月9日和2023年7月12日均为工作日，无休息日影响，即A=0。因此，计算基于贡献率的区域1负荷增长量化归因情况如表11所示。

表11 2020年7月至2023年7月区域1负荷变化量化归因

Table 11  Quantitative attribution of load changes in area 1 from July 2020 to July 2023

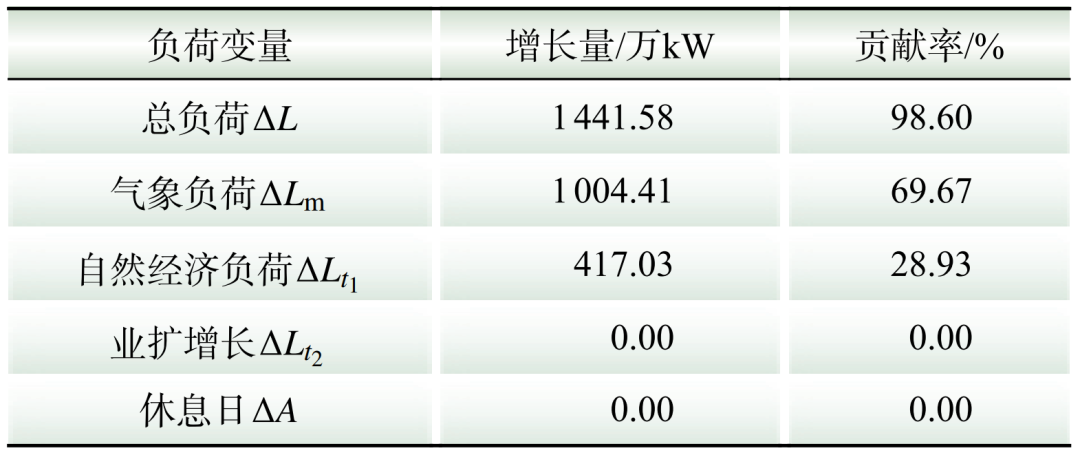
虽然各类负荷贡献率之和与理论值100%有所不同，但其差值在可接受范围之内。其中，算例1由于各类负荷解耦不充分，仍存在一定交叉，故各类负荷贡献率之和超过100%；算例2则是受限于数据原因，未考虑业扩影响，故各类负荷贡献率之和低于100%。

04

结论

本文提出了一种基于电力数据特征构建的电力负荷增长归因及量化分析方法，利用鱼骨图定性分析影响电力负荷的各种因素，结合实际采集的电力电量数据，构建了能够表征气象因素、经济因素和特殊事件的相关指标。通过对总负荷进行分解，提取气象负荷、自然经济负荷、业扩负荷、随机负荷，利用不同负荷增长对总负荷增长的贡献率，定量表征其对负荷增长的影响程度，得出如下结论。

1）该负荷增长特征构建方法能够精细化表征气象因素、经济因素和特殊事件对负荷变化产生的影响。

2）从自然经济增长的角度，提出了一种基于经济发展的自然负荷增长指标，利用产业增加值和人均消费支出对自然经济负荷的增长情况进行表征。

3）考虑产业结构对负荷的影响，提出了一种基于电力电量修正的产业结构变化指标，从不同产业电力电量所占比重的角度分析产业结构变化。

4）考虑到特殊事件对负荷的影响，通过构建事件趋势一致性评价指标来表征事件和负荷波动的关联关系。

5）利用西北2个区域的电力电量数据分别进行了较短周期和长周期算例验证。本文的分析思路和方法也适应于其他区域的负荷增长成因分析。

本文提出的负荷增长量化归因分析方法对于气象负荷以及随机负荷均采用了估算方法，后续可进一步探究更为精准的计算方法。同时，对于业扩报装产生的负荷与基础负荷、气象负荷、随机负荷解耦并不充分，仍存在部分重叠，因此对于该部分的负荷解耦，确保其能够被有效量化是后续研究需要解决的问题。此外，在不同时间尺度上各影响因素的权重如何分配也是后续研究的重点。