考虑源网协同支撑作用的含新能源电力系统网架重构决策优化方法

编者按

近年来，极端天气、人为误操作等各种因素导致大停电事故频发。同时，随着双碳目标的不断推进，中国电力系统呈现出的新能源高占比新特征为电网的安全稳定运行带来了新的挑战。研究制定新能源高比例接入下的系统恢复方案，对建立完善新型电力系统安全防御体系具有重要意义。

（来源：微信公众号《中国电力》 作者：周健，冯楠，季怡萍，冯煜尧，王帅，李少岩）

《中国电力》2024年第10期刊发了周健等撰写的《考虑源网协同支撑作用的含新能源电力系统网架重构决策优化方法》一文。文章提出一种新能源、储能、常规机组和输电网络协同恢复的网架重构优化方法。首先，基于核密度法刻画了新能源出力的不确定性，同时考虑新能源功率波动性确定其接入时机；在此基础上，引入多场站短路比指标来衡量网架强度对新能源的承载力，并通过伴随网络法实现了相应约束的线性化建模；最后，以最大化负荷恢复量和新能源出力为优化目标，建立了新能源参与下源网协同恢复的双层优化模型，并通过仿真系统验证了所提方法。

摘要

面对复杂多变的国际形势和日益增多的极端事件，研究新能源高比例接入下的系统恢复方案，对完善新型电力系统安全防御体系具有重要意义。在此背景下，提出一种含新能源电力系统网架重构决策优化方法。首先，基于核密度法对新能源出力不确定性进行分析建模；其次，考虑新能源并网和运行对网架强度的要求，实现了新能源多场站短路比约束的线性化建模；在此基础上，建立了能协同新能源、储能、常规机组和输电网络恢复的网架重构优化模型，并提出双层优化策略以提升模型求解效率。基于新英格兰10机39节点系统的算例结果验证了所提方法的有效性。

01

新能源参与系统恢复安全条件分析

1.1  新能源出力不确定性建模

目前新能源出力预测误差分布的拟合方法有参数估计和非参数估计。其中核密度估计法已有较为成熟的理论，可用于模拟风电场相邻时刻风速的联合概率分布。基于此，本节采用非参数核密度法拟合预测误差的概率分布模型，以刻画新能源出力不确定性。

假设在某一预测出力区间内的历史误差样本数据为e1, e2, ···, eN，其中N为样本数据总数，则采用核密度法估计的预测误差概率密度函数p(e)为

式中：e为新能源预测误差；h为带宽，也称平滑系数；K(·)为核函数，通常选取以0为中心的对称单峰概率密度函数，此处采用高斯核函数；ek为第k个历史误差样本。

采用正态分布和核密度法拟合的预测误差概率分布如图1所示。通过对比可见核密度法更好地刻画了新能源出力预测误差尖峰厚尾、非对称的特征，拟合结果更切近实际误差分布。

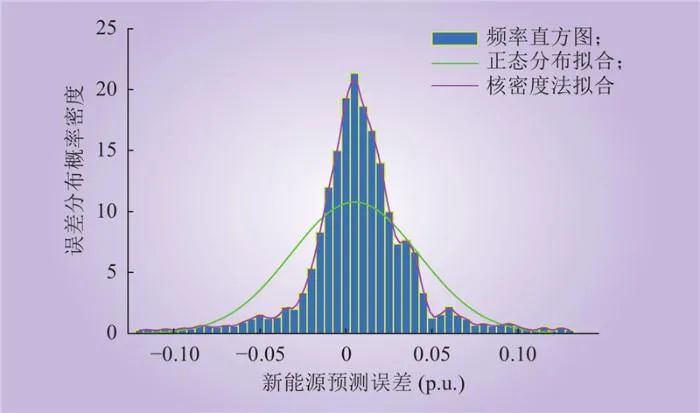
图1  新能源预测误差概率分布

Fig.1  The probability distribution of new energy prediction error

在确定出预测误差的概率分布函数后，便可求得在置信水平α下新能源出力预测误差的置信区间，即预测误差落在区间[−v,v]上的概率为α，而新能源预测出力的置信区间即为预测出力和预测误差置信区间的叠加。

通过核密度法拟合新能源出力预测误差的概率分布，实现了新能源出力不确定性的建模。在系统恢复过程中，应取某一置信水平下预测出力误差下限进行优化调度，以防新能源出力不确定性导致系统出现功率缺额，引发负荷二次失电延误系统的恢复进程。

1.2  新能源接入对网架强度的支撑要求

本节将从新能源并网和运行2个层面切入，给出新能源接入对已恢复系统的支撑强度要求。

1）系统调频能力约束。为了抵御新能源接入时的功率冲击，已恢复系统需具备足够的调频能力。现假定各新能源场站错时启动，则新能源安全接入的稳态频率约束为

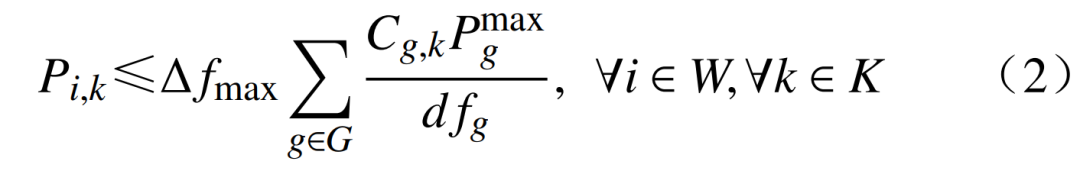
式中：Pi,k为节点i上新能源场站在第k时步的有功出力；Cg,k为机组g在第k时步并网状态的0-1变量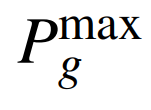；为机组g的额定有功功率；dfg为机组g的频率响应值；Δfmax为系统允许的最大稳态频率偏差，一般取0.5 Hz；G为所有常规机组的集合；W为新能源场站所在节点的集合；K为恢复时步的集合。

2）网架电压支撑能力约束。本节通过新能源多场站短路比指标以衡量已恢复网架的电压支撑强度，确保各新能源场站的接入量与系统的网架强度相匹配，保障系统恢复进程的安全推进，即

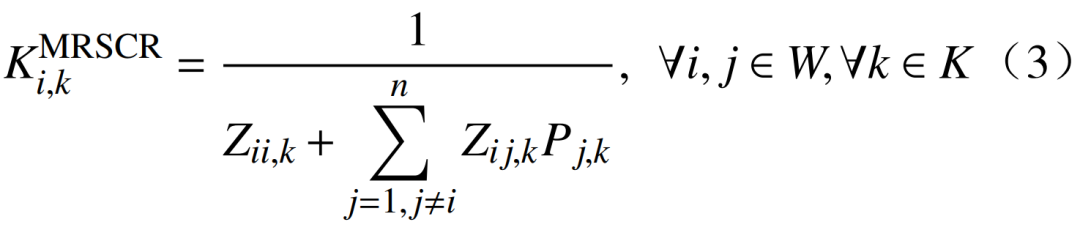
式中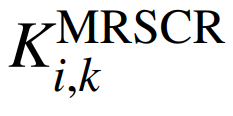：为节点i第k时步的多场站短路比指标；Zii,k为节点i在第k时步的自阻抗；Zij,k为第k时步节点i、j间的等值互阻抗；Pi,k和Pj,k分别为节点i、j上新能源场站第k时步的有功出力。

本节参考文献[18]的建模思路，通过构建与恢复网架动态映射的伴随网络，实现多场站短路比约束的线性化建模。根据网络节点电压方程U=ZI，给各新能源场站所在节点注入其出力大小的电流源，其余节点均不注入电流，则各新能源场站所在节点的电压值为节点阻抗元素与新能源功率乘积的线性组合。新能源多场站短路比约束的线性化建模为

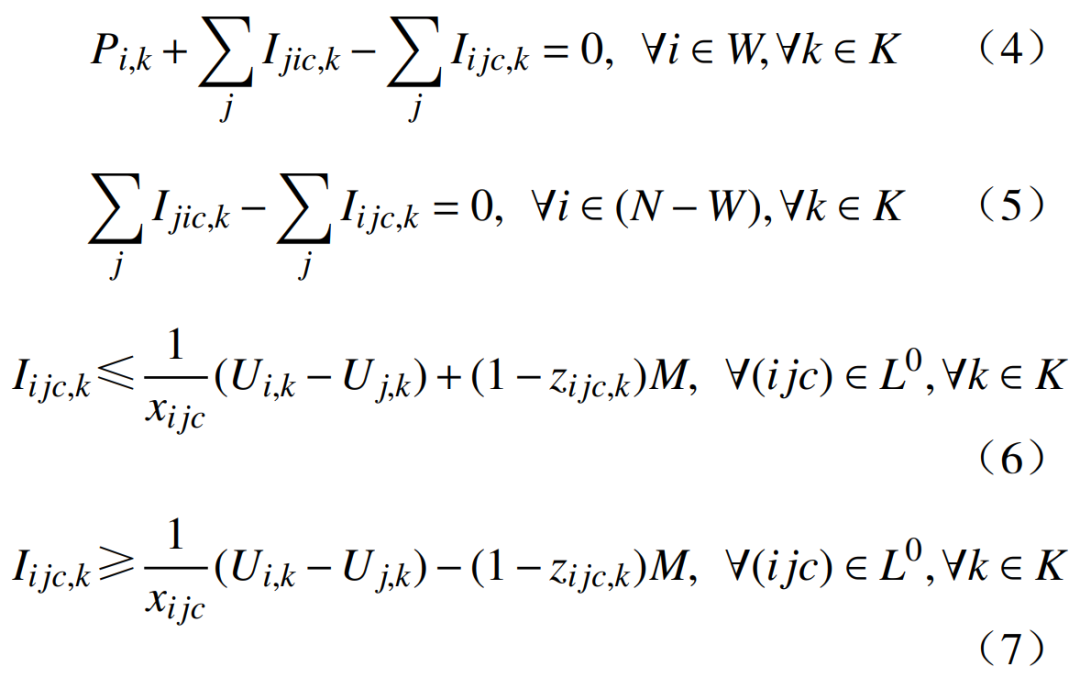
式中：Iijc,k和Ui,k分别为伴随网络中第k时步线路i-j-c上的电流值和节点i上的电压值；xijc为线路i-j-c的电抗值；Di,k和zijc,k分别为表示第k时步节点i上新能源场站并网状态和线路i-j-c投运状态的0-1变量；M为一个很大的正数；L0为包含发电机接地支路在内的线路集合；N为所有节点集合。

02

多源协同恢复的网架重构优化模型

2.1  各类型电源的解析化建模

1）风电与光伏运行约束为

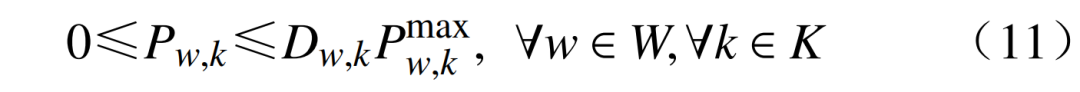
式中：Pw,k为风电和光伏在第k时步的运行出力；Dw,k为表示风电和光伏在第k时步并网状态的0-1变量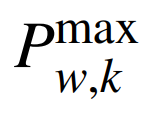；为风电和光伏在第k时步的调度上限，预测出力置信区间的下限。

此外新能源出力还具有波动性，其接入时机应确保已恢复系统具备足够的功率调节能力。为避免系统再次失负荷风险，新能源场站的并网时机约束为

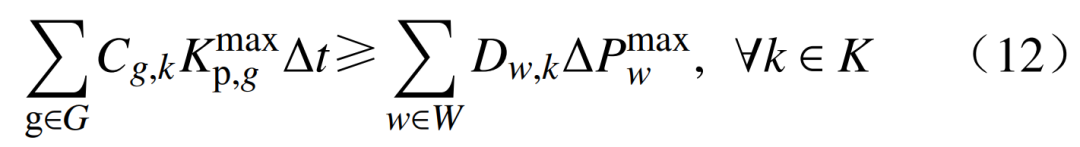
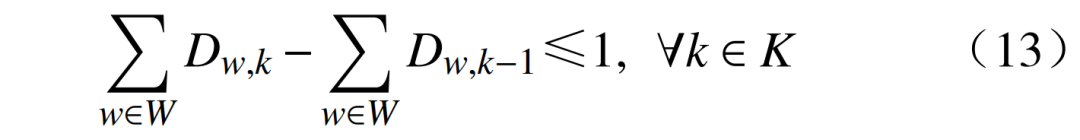
式中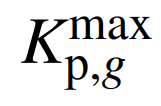：为机组g的最大爬坡率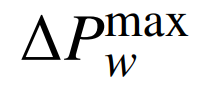；为新能源场站w预测出力的最大波动功率；Δt为恢复时步的时长。

2）常规机组及快速甩负荷（fast cut back，FCB）机组的运行约束为

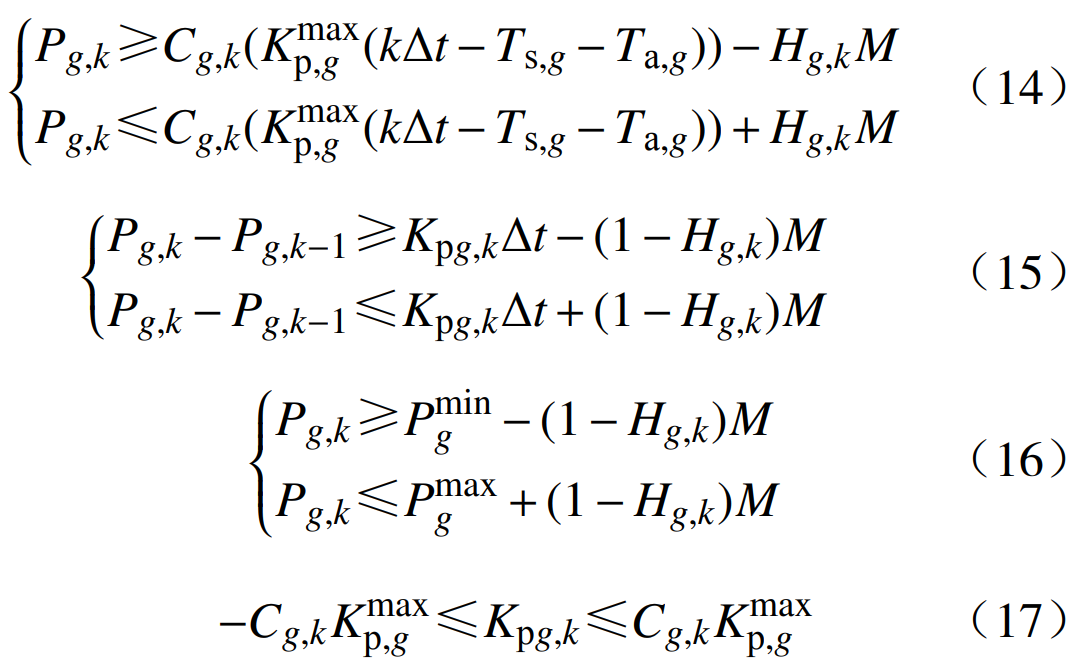
式中：Pg,k为机组g在第k时步的运行出力；Ts,g为机组g的启动时刻；Ta,g为机组g从启动到并网的时长；Hg,k为机组g在第k时步稳燃状态的0-1变量；Kpg,k为机组g在第k时步的爬坡率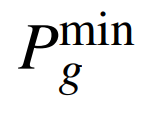；为机组g维持稳燃的最小出力。

此外，常规机组还需考虑机组启动功率及冷热启动时间约束。而具备FCB功能的机组，在电网停电后，能维持厂用电负荷供电下平稳运行，无需外部电源提供启动功率，无冷热启动时间限制。本文采用FCB机组作为黑启动电源，并取其启动时刻作为系统恢复过程的起始时刻。

3）储能电站运行约束。本文通过考虑储能电站的荷电量状态和充放电功率来刻画其在系统恢复过程中的运行约束。具体参考文献[20]。

2.2  源网协调恢复的网架重构决策模型

本文网架重构优化模型以系统的负荷恢复量和新能源出力最大化作为优化目标f。其中α为权重系数，取值范围为0~1，可根据各阶段系统恢复程度动态调整，促使新能源机组尽快并网，即

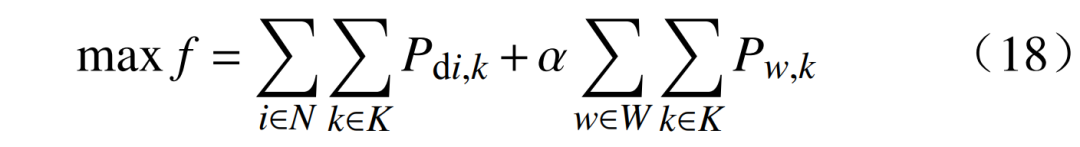
1）无功和自励磁约束为

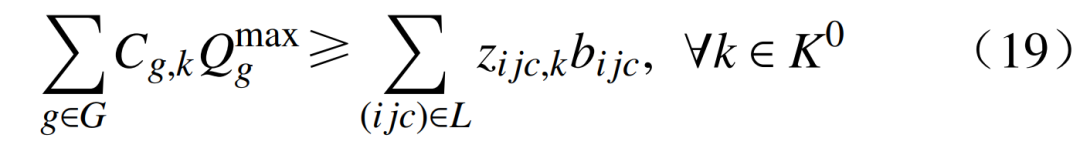
式中：为机组g空载时所能吸收的最大无功；bijc为线路i-j-c的充电电容；K0为恢复初期的时步集合。

2）其它约束。在系统恢复过程中，主要的约束条件包括系统功率平衡、线路潮流及网架连通性等约束。为计及电压和无功对系统恢复过程的影响，本文采用线性化交流潮流。为确保网架的连通性，可根据网络流理论建立连通性约束。另外，对于长时间尺度的网架重构过程，还需考虑系统恢复状态与决策变量间的映射关系及时步间的边界条件。

03

模型的双层优化求解策略

首先，针对机组爬坡模型中关于时间分段的0-1变量，如机组的启动状态、并网状态及稳燃状态，可通过大M法进行线性化处理。此外，若在网架重构全局优化模型中考虑多场站短路比约束将导致模型的求解时长急剧增长，不利于模型在大规模电力系统中的应用。因此，本节提出优化模型的双层优化策略，针对机组启动次序和恢复路径进行迭代求解，求解流程如图2所示。

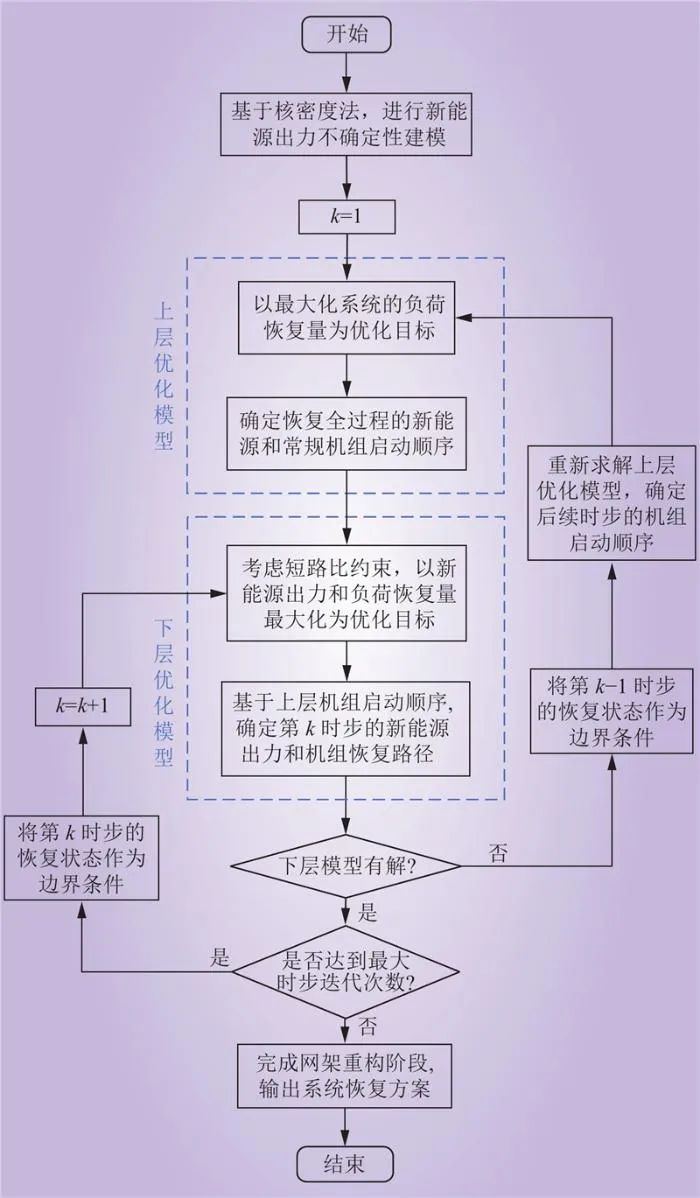
图2  双层优化模型求解流程

Fig.2  Bi-level optimization model solving process

首先不考虑新能源多场站短路比约束，建立全过程网架重构的上层优化模型，根据风光储及常规机组自身运行特性，结合系统功率平衡、线路潮流、网络连通性等约束，确定出新能源场站和常规机组的全过程启动次序。然后，基于上层优化模型确定的机组启动顺序，追加多场站短路比约束建立单时步网架重构的下层优化模型，通过合理调整网架拓扑确定机组的送电路径，能有效提升网架对新能源的承载能力，充分挖掘各新能源场站对系统恢复的功率支援作用。若下层模型出现无解，表明上层机组启动次序不可行，则需更新当前恢复时步的边界条件，返回上层优化模型重新求解后续时步的机组启动次序，以此类推迭代求解可得出全过程的恢复方案。

04

算例分析

4.1  参数设置

本文采用新英格兰10机39节点系统进行仿真，现选取节点30的FCB机组作为黑启动电源，所有机组相关参数如表1所示，其中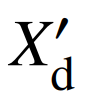为各机组接地支路对应的暂态电抗值，节点32所接机组的冷启动时限设为2 h。光伏电站和风电场各时步预测出力曲线如图3所示。两个储能电站的规模分别为50 MW/100 MW·h和100 MW/200 MW·h，相应的充放电功率为20~50 MW和40~100 MW，充放电效率均为0.95，初始荷电量分别为30%和40%，荷电量上下限均为10%和90%。

表1  新英格兰10机39节点系统机组参数

Table 1  Unit parameters of New England 10-unit 39-bus system

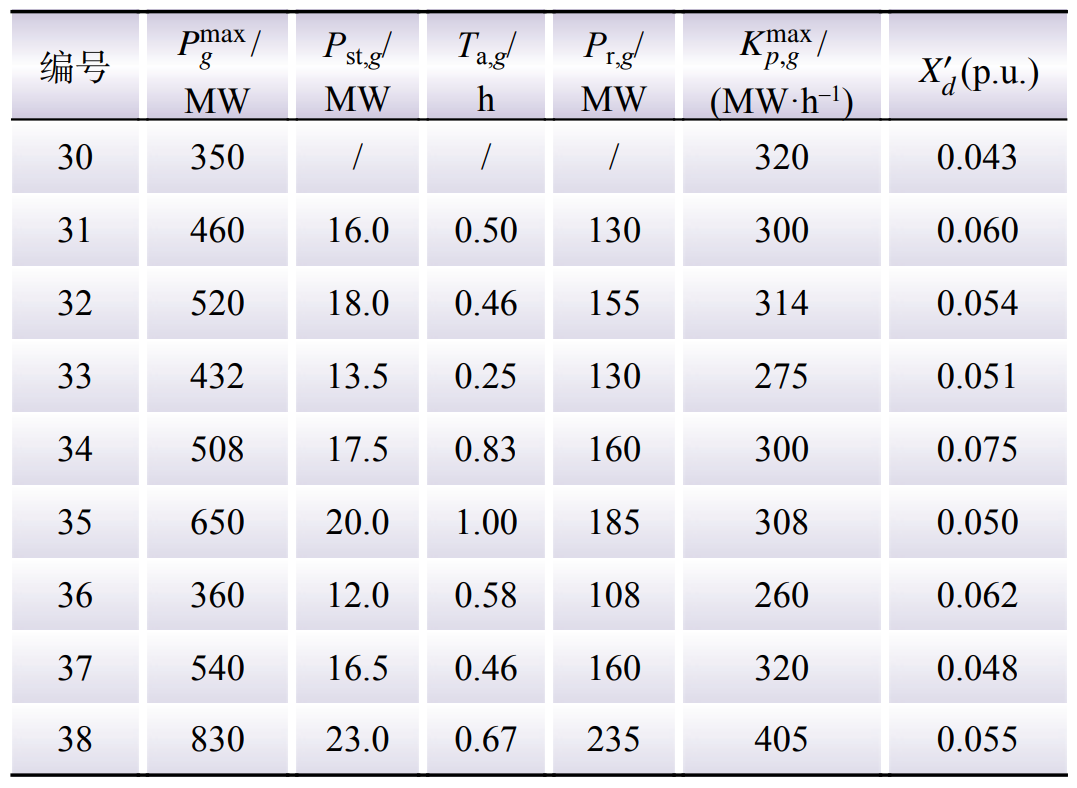
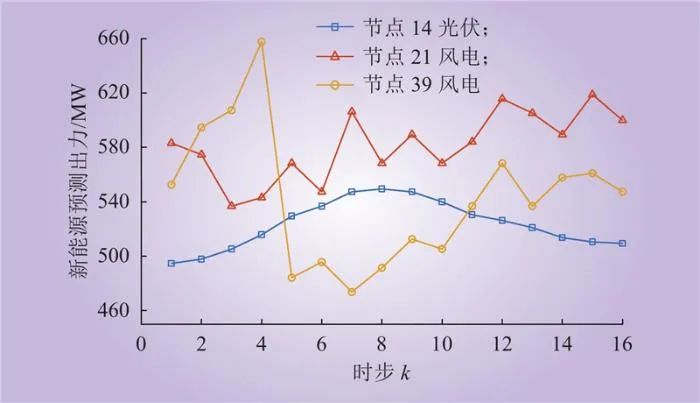
图3  新能源预测出力曲线

Fig.3  New energy forecast output curve

4.2  源网协同恢复的网架重构方案

为了说明本文所提双层优化方法的有效性，采用全局优化方法作为对比方案。在整个网架重构过程中，双层优化方案的负荷恢复量略低于全局优化方案3.1%，但求解总时长仅为192 s，远小于全局优化方案长达1.5 h的求解耗时。由此可见，双层优化策略在保证全局优化效果的前提下大幅提升了模型的求解效率，更有利于实际工程应用。现以所有机组并网作为网架重构阶段的结束，给出双层优化的系统恢复方案，最终形成的骨干网架如图4所示。具体各时步恢复数据如表2所示。

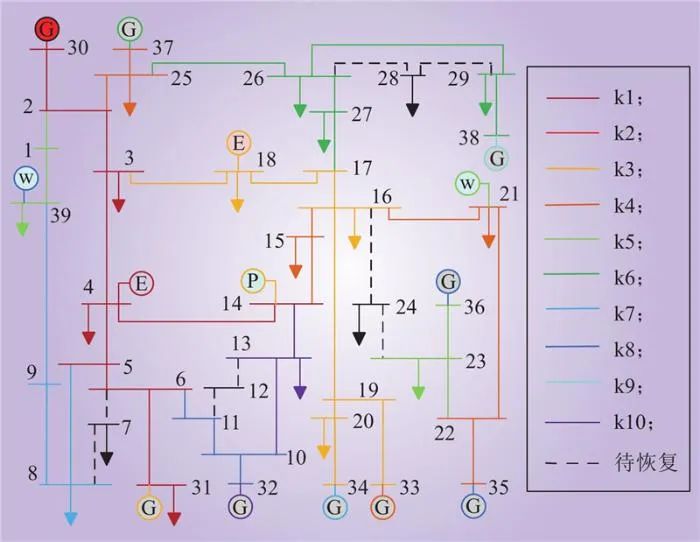
图4  新英格兰10机39节点系统的网架重构方案

Fig.4  The grid reconstruction scheme of New England 10-machine 39-node system

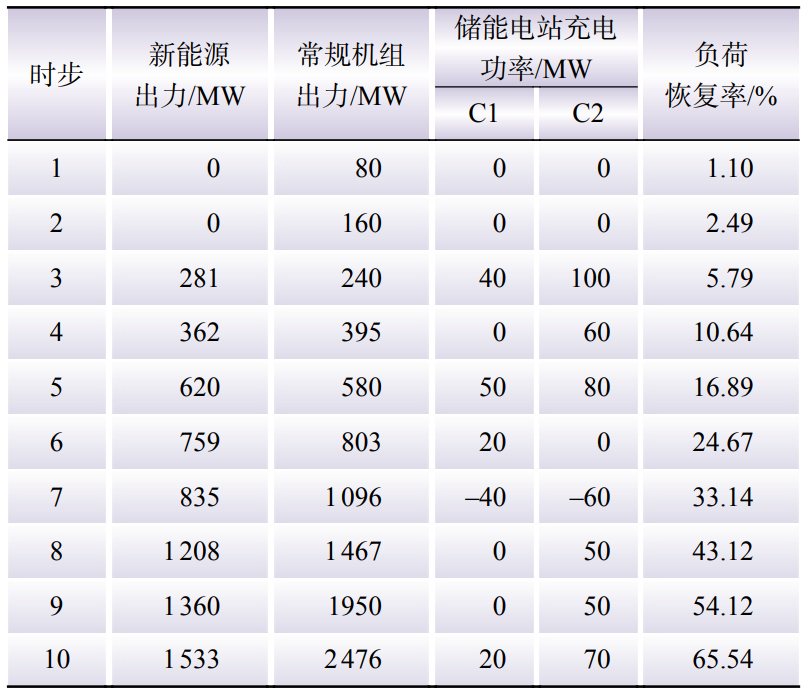
表2  各时步恢复数据

Table 2  The restoration data of each time step

由图4可见，在系统恢复的第1时步仅投运了7条线路，主要是由于投运空载线路产生的充电无功，仅有黑启动机组进相运行来吸收，这说明网架重构初期线路的投运操作主要受系统无功问题的制约。直至第3时步，机组31并网运行以及负荷逐步恢复提升了系统调频能力及无功吸收能力，才有新的线路投运。后续时步随着机组的陆续并网和线路投运，负荷恢复速率将逐步提升，直至第10时步冷启动机组32并网，完成了系统恢复的网架重构阶段。

4.3  新能源安全并网和运行约束的有效性分析

本文从网架支撑强度和系统调频能力两个层面，对恢复过程中新能源的并网时机和接入量进行量化评估，现针对所得优化方案进行分析说明。

新能源场站各时步的具体出力如图5所示。第3时步，系统的功率调节能力足以应对新能源出力波动性，节点14的光伏电站并网运行向系统提供功率支撑。第4时步，线路14-15、15-16投运形成局部环网，网架强度得到进一步增强。第5时步，节点21的风电场并网，新能源出力大幅提升加快了系统恢复进程。之后两个新能源场站在多场站短路比约束下功率稳步提升，充分挖掘了源网的协同支撑作用。直至第8时步，由于机组35和36的并网，提升了系统的功率调节能力，节点39的风电场安全接入电网。第10时步，机组32并网后，网架强度足以支撑新能源的全部出力，各新能源场站在预测值的制约下最大程度发挥其功率支援作用。

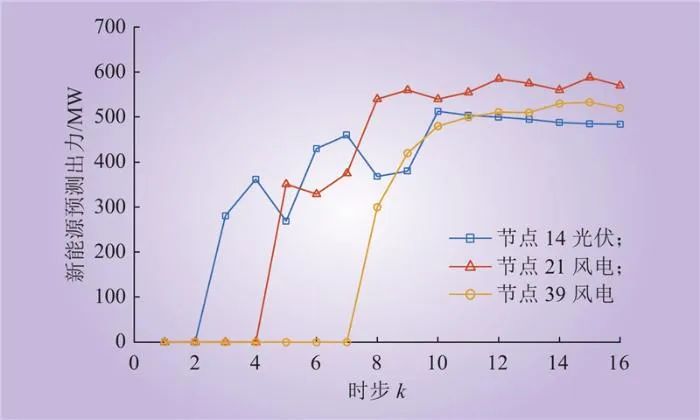
图5  新能源调度出力曲线

Fig.5  New energy dispatching output curve

值得注意的是，各新能源场站是根据其波动性由小至大依次并网，有效避免了新能源出力向下波动而引发系统二次失负荷的风险。此外，为避免新能源出力不确定性对系统恢复的影响，本文取新能源预测误差的置信水平为0.9，给调度出力和预测出力之间留有一定的裕度。

网架重构阶段各时步的新能源多场站短路比指标如图6所示由于恢复初期系统调频能力不足，负荷投运量受到限制，新能源出力无法被充分利用，故光伏电站并网后前三个时步短路比指标大于3。随着恢复进程的推进，系统调频能力不断增强，单时步负荷投运量足以消纳新能源出力，则各新能源场站在多场站短路比约束下最大程度发挥各自的功率支援作用。上述结果说明，在系统恢复过程中新能源接入量受到机组调频能力和网架支撑强度的双重制约，而本文所提模型能充分考虑源网的协同支撑作用，最大化挖掘系统网架调控潜力以提升新能源接入功率。

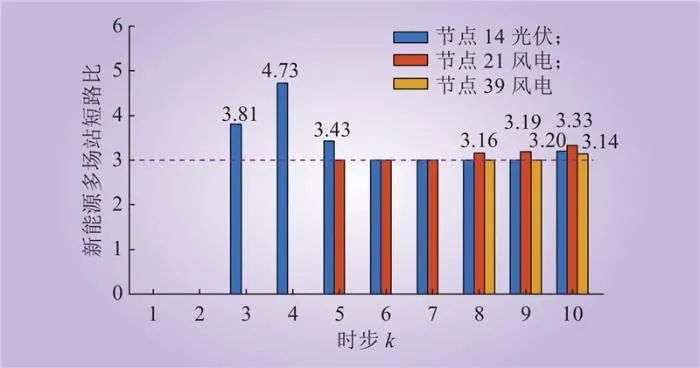
图6  各时步新能源多场站短路比指标

Fig.6  The multiple renewable energy stations short-circuit ratio index at each time step

05

结论

针对多类型电源参与下的系统恢复方案制定，本文提出了一种能够兼顾新能源、常规机组和线路恢复的网架重构决策优化方法。通过算例分析，得出以下结论：

1）本文针对新能源出力不确定性及波动性的分析建模，能有效避免系统恢复过程中产生功率缺额引发的二次失负荷风险；

2）各新能源场站的并网时机及运行出力与系统调频能力和网架支撑强度动态配合，充分挖掘了源网协同支撑对新能源承载力的提升作用；

3）针对网架重构决策优化模型，分别确定机组启动顺序和恢复路径的双层求解策略，大幅提升了优化模型的求解效率，有利于工程应用。

注：本文内容呈现略有调整，如需要请查看原文。